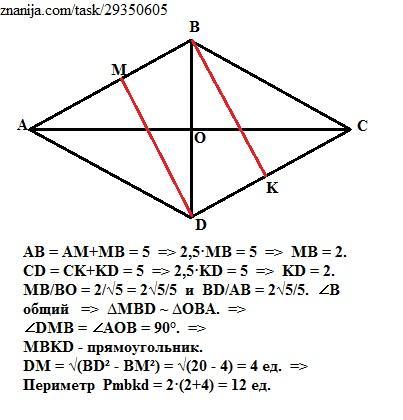
В ромбе ABCD AB=5, BD=2√5 на сторонах ab и cd отмечены точки m и к соответственно так, что AM/MB = CK/KD = 1,5. Докажите, что MBKD - прямоугольник и найдите его периметр и площадь.
Ответы
Ответ:
Pmbkd = 12 ед.
Доказательство в приложении.
Объяснение:
В ромбе все стороны равны, а диагонали взаимно перпендикулярны.
Дано, что AM/MB = CK/KD = 1,5. =>
АМ=1,5·MВ; СК = 1,5·KD.
АВ = АМ+МВ = 5 => 2,5·MB = 5 => MB = 2.
CD = CK+KD = 5 => 2,5·KD = 5 => KD = 2.
MB║KD как части противоположных мторон ромба.
Значит MBKD - параллелограмм по признаку: "Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм".
Рассмотрим треугольники МВD и АВО.
МВ/ВО = 2/√5 = 2√5/5 и ВD/AB = 2√5/5.
Итак, в этих треугольниках стороны пропорциональны, а углы, заключенные между этими сторонами, равны (угол В - общий).
Следовательно, эти треугольники подобны, а так как треугольник АВО прямоугольный, то и треугольник MBD - прямоугольный.
В параллелограмме MBKD угол MDB - прямой (доказано выше), значит четырехугольник MBKD - прямоугольник.
По Пифагору найдем сторону DM:
DM = √(BD² - BM²) = √(20 - 4) = 4 ед. =>
Периметр Pmbkd = 2·(2+4) = 12 ед.