Question

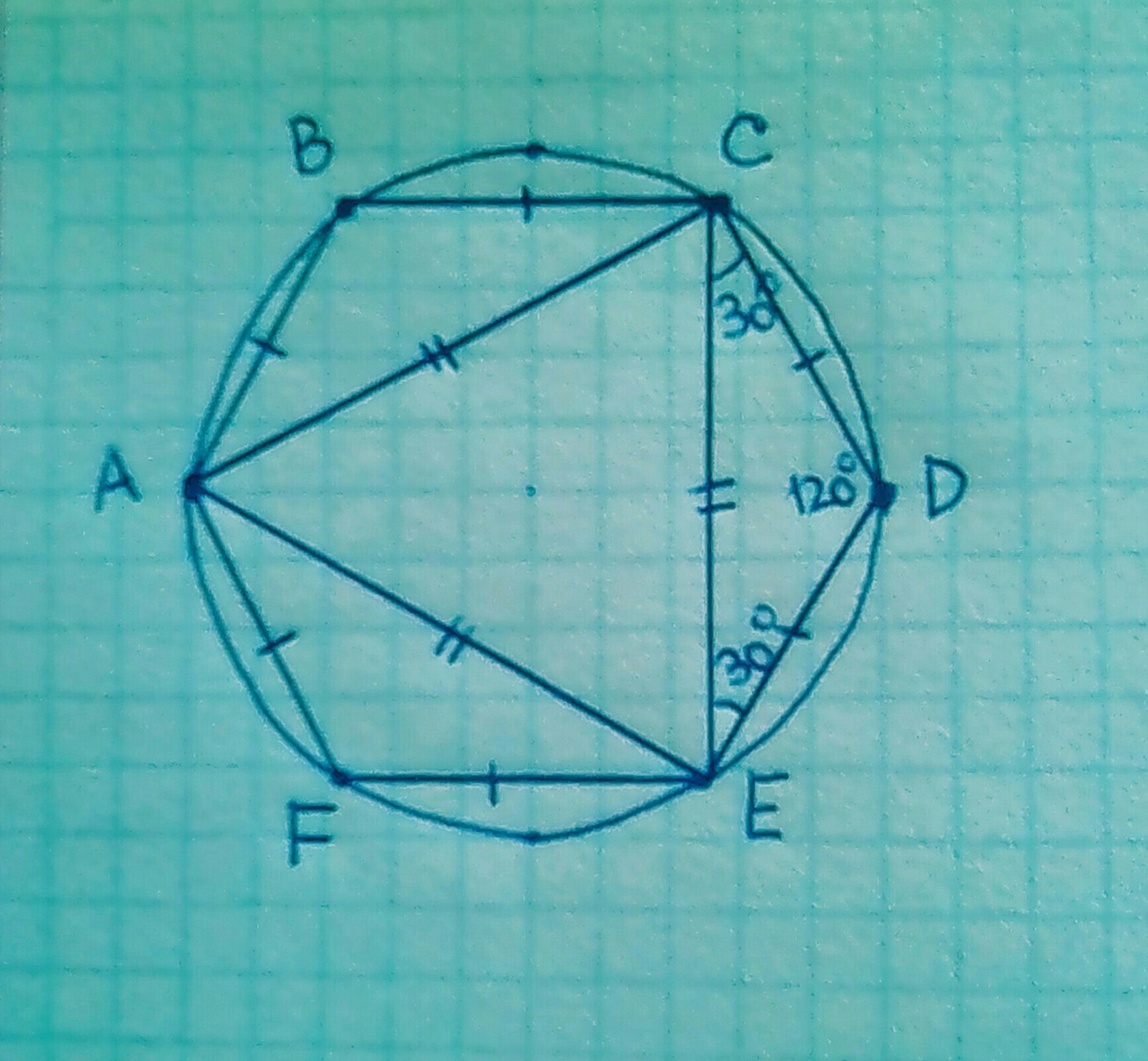
В круг вписан правильный шестиугольник и треугольник . Найдите отношение площадей шестиугольника и треугольника

Answer 1

Пусть стороны шестиугольника равны а

Все углы шестиугольника равны 120°

1) Рассмотрим ∆ СDE ( CD = DE ) :

По теореме синусов имеем:

$\frac{a}{sin30} = \frac{ce}{sin120}$

$ce = \frac{a \times sin120 }{sin30} = \frac{a \times \frac{ \sqrt{3} }{2} }{ \frac{1}{2} } = \\ \\ = \frac{a \times \sqrt{3 } \times 2}{2} = a \sqrt{3}$

Площадь правильного шестиугольника равна:

S = 3√3a² / 2

Площадь правильного треугольника равна:

S = 3√3а² / 4

Отношение равно =>

( 3√3а²/ 2 ) : ( 3√3а²/4 ) = ( 3√3а² / 2 ) × ( 4 / 3√3а² ) = 4 / 2 = 2 / 1

Значит, площадь правильного шестиугольника в два раза больше площади правильного треугольника


ОТВЕТ: 2 : 1