Предмет: Алгебра,
автор: Ilnaraaa
Помогите пожалуйста решить
Приложения:
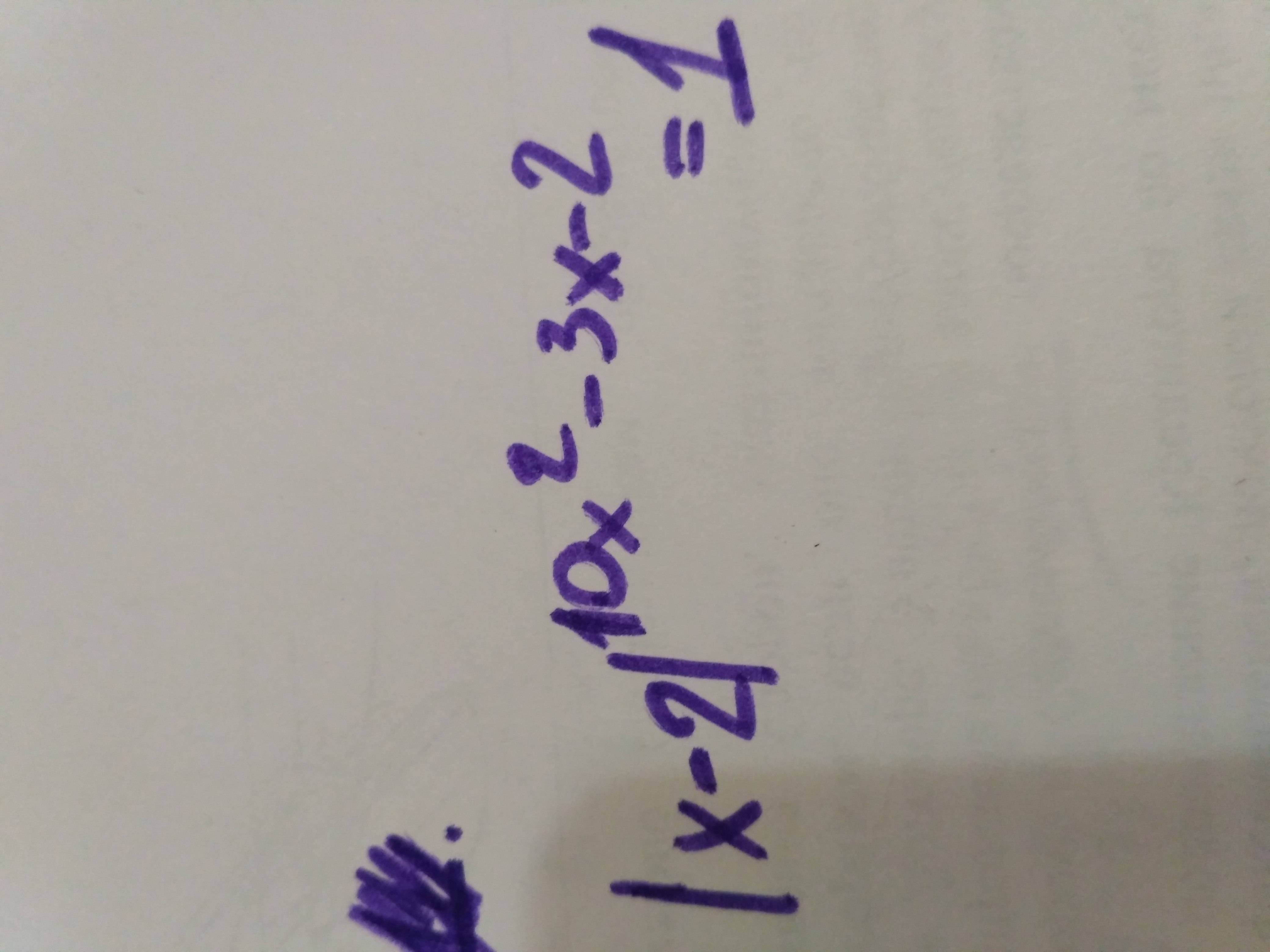
Ответы
Автор ответа:
0
Область определения x≠2, потому что основание степени |x-2| должно быть >0,
(а модуль по определению ≥0)
Если степень выражения =1, то эта степень равна =0
10x²-3x-2=0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = (-3)·2 - -4·10·(-2) = 9 + 80 = 89
x1 = (3 - √89)/(20)
x2 =( 3 + √89)/(20)
И кроме того, если степень выражения =1, то, основание степени =1
|x-2|=1, что распадается на два уравнения
x-2=1 при x≥2, откуда
x3=3
-(x-2)=1 при x<2, откуда
x4=1
Ответ:
x1 = (3 - √89)/(20)
x2 =( 3 + √89)/(20)
x3=3
x4=1
Похожие вопросы