Question

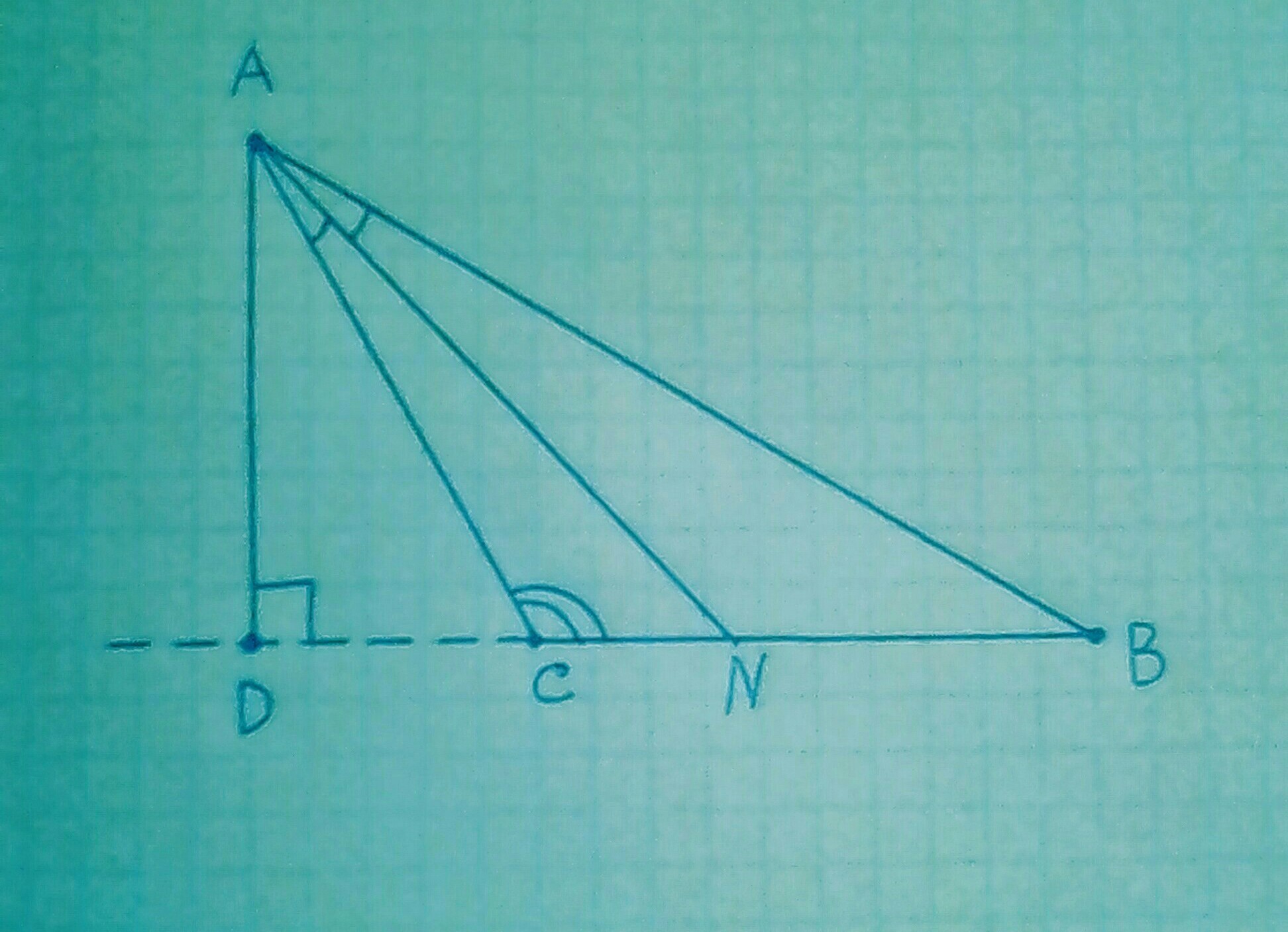
В треугольнике АВС С = 126 °, AD и AN - высота и биссектриса треугольника соответственно, DAN = 48 °. Найти углы треугольника АВС.

Answer 1

1) угол АСВ + угол АСD = 180° - по свойству смежных углов

угол АСD = 180° - 126° = 54°

2) Рассмотрим ∆ АСD ( угол ADC = 90° ):

Сумма острых углов в прямоугольном треугольнике всегда равна 90°

угол DAC = 90° - 54° = 36°

угол САN = угол DAN - угол DAC = 48° - 36° = 12°

3) AN - биссектриса =>

угол ВАС = 2 × угол CAN = 2 × 12° = 24°

4) Рассмотрим ∆ АВС:

Сумма всех углов в любом треугольнике всегда равна 180°

угол АВС = 180° - 126° - 24° = 180° - 150° = 30°



ОТВЕТ: 24° , 30° , 126°