Question

Помогите пожалуйста решить задачу!

Answer 1

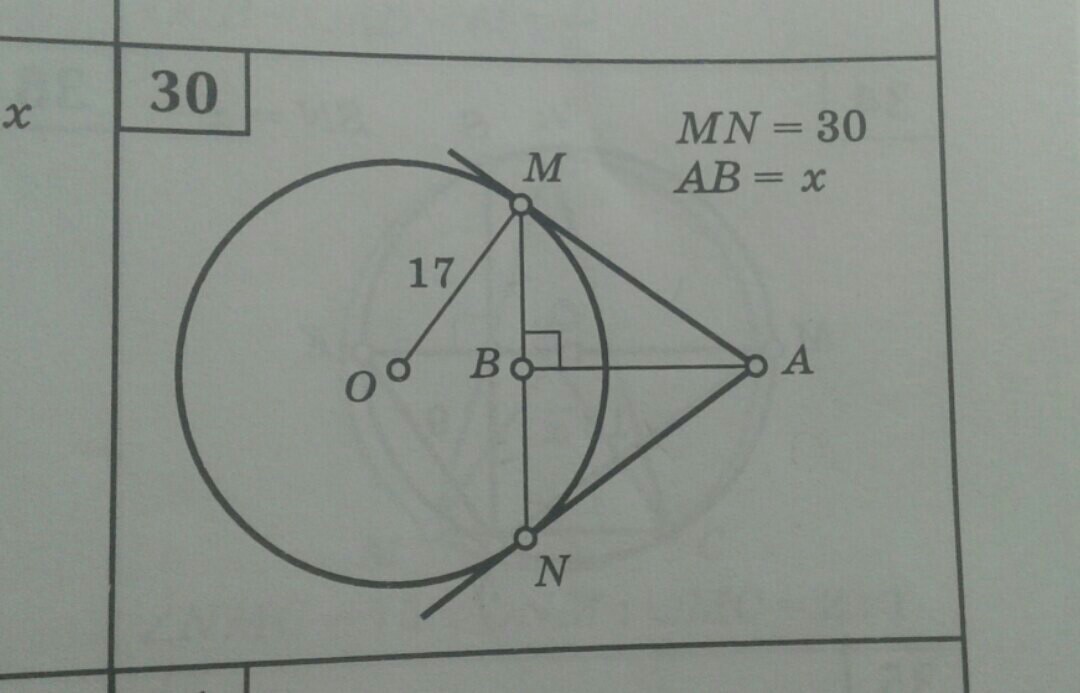
Поскольку окружность вписана в угол MAN, то её центр (О) принадлежит биссектрисе, АО, угла MAN. МА = AN (как отрезки кассателных, проведённых к окружности из одной точки), отсюда ΔAMN - равнобедренный, ВА - его высота, медиана и биссектриса (В - средина MN). Рассмотрим прямоугольный треугольник МОВ, у которого ОМ = 17, МВ = 0,5МN = 15, отсюда ОВ = 8 (17, 15, 8 - Пифагорова тройка). Треугольник ОМА - прямоугольный (угол ОМА = 90 градусов, ОМ и МА перпендикулярны как радиус и касcательная) МВ - его высота. Воспользовавшись свойством высоты прямоугольного треугольника, опущенной на гипотенузу, имеем МВ² = ОВ · ВА; ВА = МВ² : ОВ = 225 : 8 = 28,125.

Ответ: 28,125.

Answer 2

Решение на рисунке.

Если будут вопросы — задавайте.