Предмет: Геометрия,
автор: rushilddrake228568
В трапеции ABSD (AD параллельно BC) диагонали AC и BD перпендикулярны друг другу, AC=5 и BD=13. Найти расстояние между серединами оснований
Ответы
Автор ответа:
11
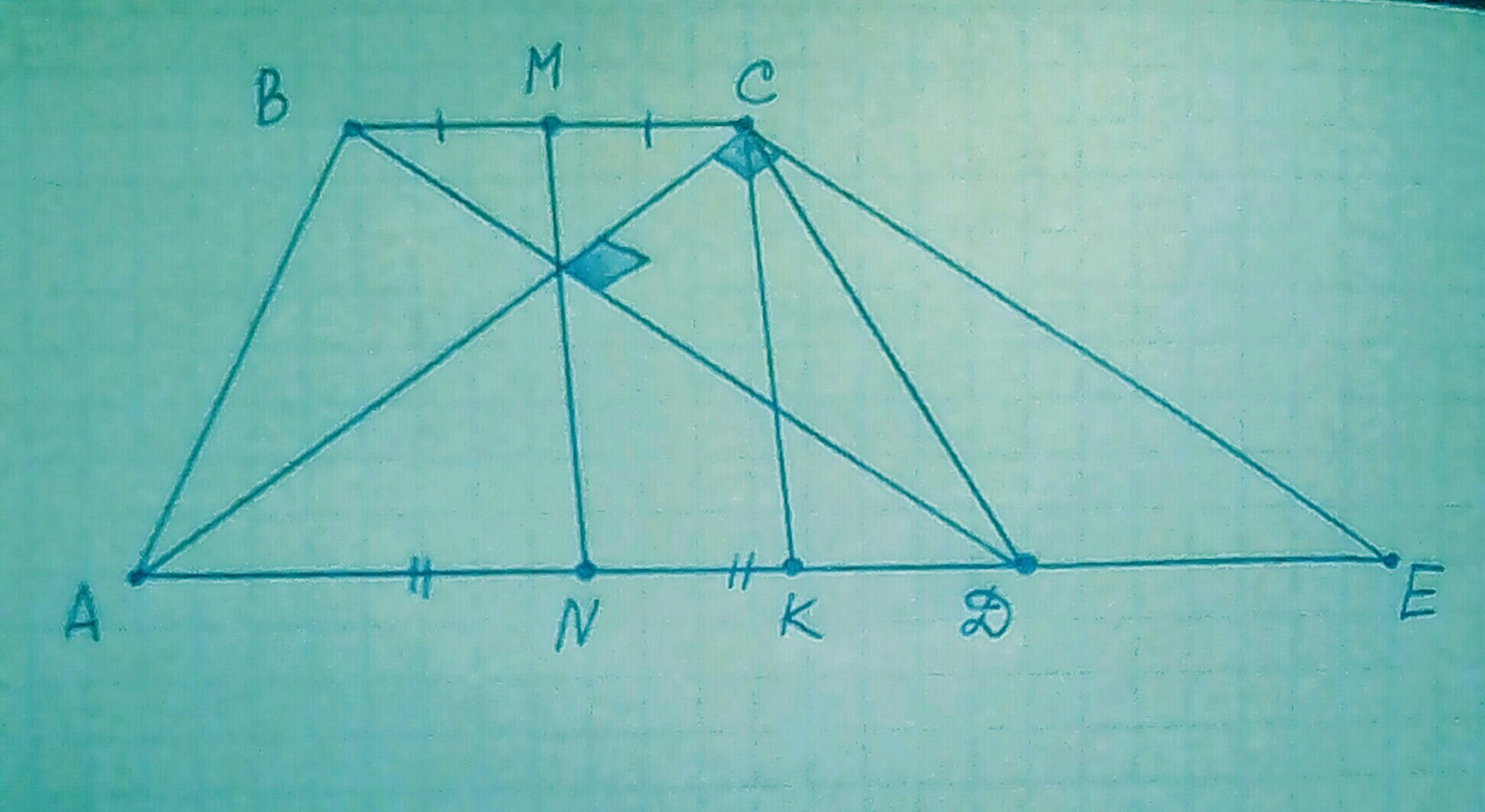
1) Осуществим дополнительное построение:
Проведём отрезок СЕ параллельно диагонали ВD => AC перпендикулярен СЕ
Проведём отрезок СК параллельно отрезку МN
Из этого следует, что четырёхугольник ВСЕD - параллелограмм ( СЕ || ВD , BC || DE ).
Aналогично, четырёхугольник МСКN - параллелограмм ( CK || MN, МС || KN )
Поэтому, BC = DE , MC = NK, BD = CE = 13
AE = AD + DE = AD + BC
AK = AN + NK = 1/2 × AD + 1/2 × BC = 1/2 × ( ВС + AD )
Значит, K - середина отрезка АЕ , АК = КЕ
Поэтому, МN = CK - медиана в ∆ АСЕ
2) Рассмотрим ∆ АСЕ ( угол АСЕ = 90° ):
" В прямоугольном треугольнике медиана равна половине гипотенузы "
По теореме Пифагора:
AE² = 13² + 5² = 169 + 25 = 194
AE = √194
Значит, искомый отрезок MN, равный отрезку СК, имеет длину:
СК = MN = 1/2 × AE = 1/2 × √194 = √194 / 2
ОТВЕТ: √194/2
Приложения:
Похожие вопросы
Предмет: История,
автор: bugansofi47
Предмет: Биология,
автор: petrovanasta969
Предмет: Обществознание,
автор: TupoyBao
Предмет: Математика,
автор: Человек2525
Предмет: Биология,
автор: СоусГласс