Предмет: Алгебра,
автор: 1356953336975
3. Постройте график функции

. Какова область определения функции? При каких значениях х функция принимает отрицательные значения?
Приложения:
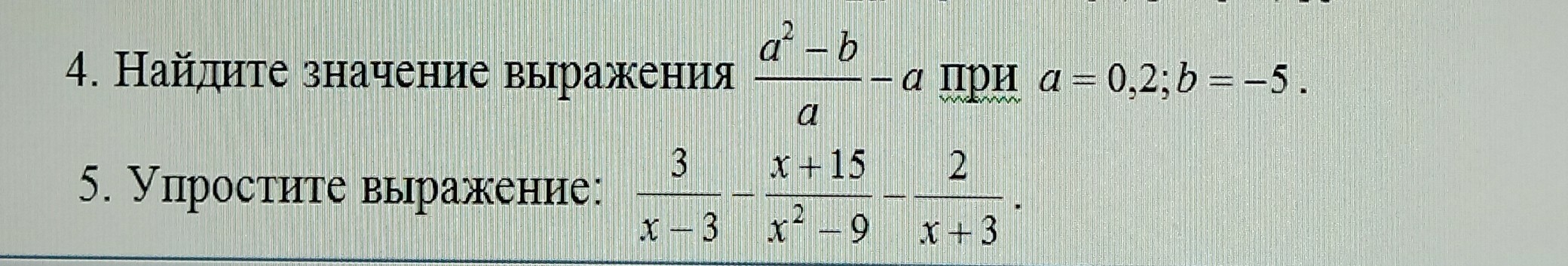
Ответы
Автор ответа:
1
3) График во вложении.
Область определения: (-беск; 0) U (0; +беск)
Функция принимает отрицательные значения при (-беск; 0).
4)

при a = 0,2; b = -5

5)

Область определения: (-беск; 0) U (0; +беск)
Функция принимает отрицательные значения при (-беск; 0).
4)
при a = 0,2; b = -5
5)
Приложения:

Похожие вопросы
Предмет: Другие предметы,
автор: pickinganame
Предмет: Русский язык,
автор: amina9900
Предмет: Математика,
автор: olivoliv035
Предмет: Математика,
автор: 20162008
Предмет: История,
автор: dslepakova18