Решите пожалуйста уравнение 8-9 класса. Буду очень признателен и одарю баллами!
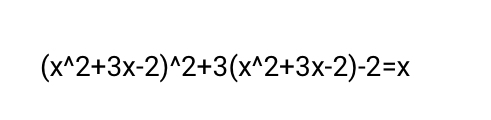
Ответы
(x²+3x-2)² +3(x²+3x-2) - 2 = x
(x²+3x-2)² +3(x²+3x-2) - 2 - x =0
1) Отдельным действием выполним возведение трехчлена в степень
(x²+3x-2)² = (x²)² + 2 · х² ·(3x-2) + (3х-2)² = х⁴+6х³-4х²+9х²-12х+4 =
= х⁴+6х³+5х²-12х+4
2) А теперь подставим и решаем.
х⁴+6х³+5х²-12х+4 +3x²+9x-6 - 2 - x =0
х⁴+6х³+8х²-4х-4 = 0
(х⁴ + 6х³ + 9х²) - 9х² + 8х² - 4х - 4 = 0
((х²)² + 2·х² · 3х + (3х)²) - х² - 4х - 4 = 0
(х²+3х)² - (х²+4х+4) = 0
(х²+3х)² - (х+2)² = 0 - разность квадратов.
(х²+3х-х-2)·(х²+3х+х+2) = 0
(х²+2х-2)·(х²+4х+2) = 0
Получаем два квадратных уравнения:
х²+2х-2 = 0 и х²+4х+2 = 0
Решаем первое:
х²+2х-2 = 0
D = 4-4·1·(-2) = 4+8=12; √D = 2√3;
x₁ = (-2-2√3)/2 = - 1 - √3
x₂ = (-2+2√3)/2 = - 1 + √3
Решаем второе:
х²+4х+2 = 0
D = 16-4·1·2 = 8; √D = 2√2
x₃ = (-4-2√2)2 = -2-√2
x₄ = (-4+2√2)2 = -2+√2
Ответ: {-2-√2; -1-√3; -1+√3; -2+√2 }
Рассмотрим функцию уравнение имеет вид f(f(x))=x. Если бы f(x) монотонно возрастала, уравнение было бы равносильно f(x)=x. В нашем случае это не так. Но по любому решения уравнения f(x)=x являются решениями и уравнения f(f(x))=x. Решим уравнение f(x)=x;
Теперь для нахождения оставшихся двух корней (если они есть) нужно разделить исходный многочлен
на
в результате получаем частное Ищем его корни:
Ответ: