Question

Радиус шара =12 см. Через конёк радиуса проведена плоскость под углом 60 градусов. Найдите площадь сечения.

Answer 1

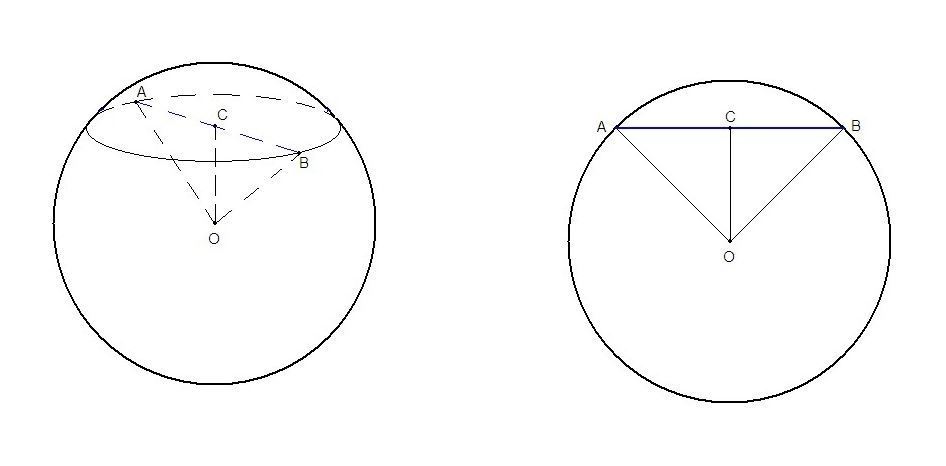
Сечение шара - круг. Пусть С - его центр, АВ - диаметр сечения.

ОС - отрезок, соединяющий центр шара с центром сечения, поэтому перпендикулярен сечению.

Тогда ВС - проекция радиуса ОВ на плоскость сечения.

Значит, ∠ОВС = 60° - угол между плоскостью сечения и радиусом шара.

ΔАОВ - равнобедренный (ОА = ОВ = R), значит

∠ОАС = ∠ОВС = 60°, тогда ∠АОВ = 60°.

AC = BC = AO/2 = 12/2 = 6 (По свойству прямоугольного треугольника: катет прилежащий углу 60° равен половине гипотенузы).

r = АС = АВ/2 = 6 см

S = πr² = π·6² = 36π см²