Предмет: Математика,
автор: zerol1231
Пожалуйста
Решите неравенство
Приложения:
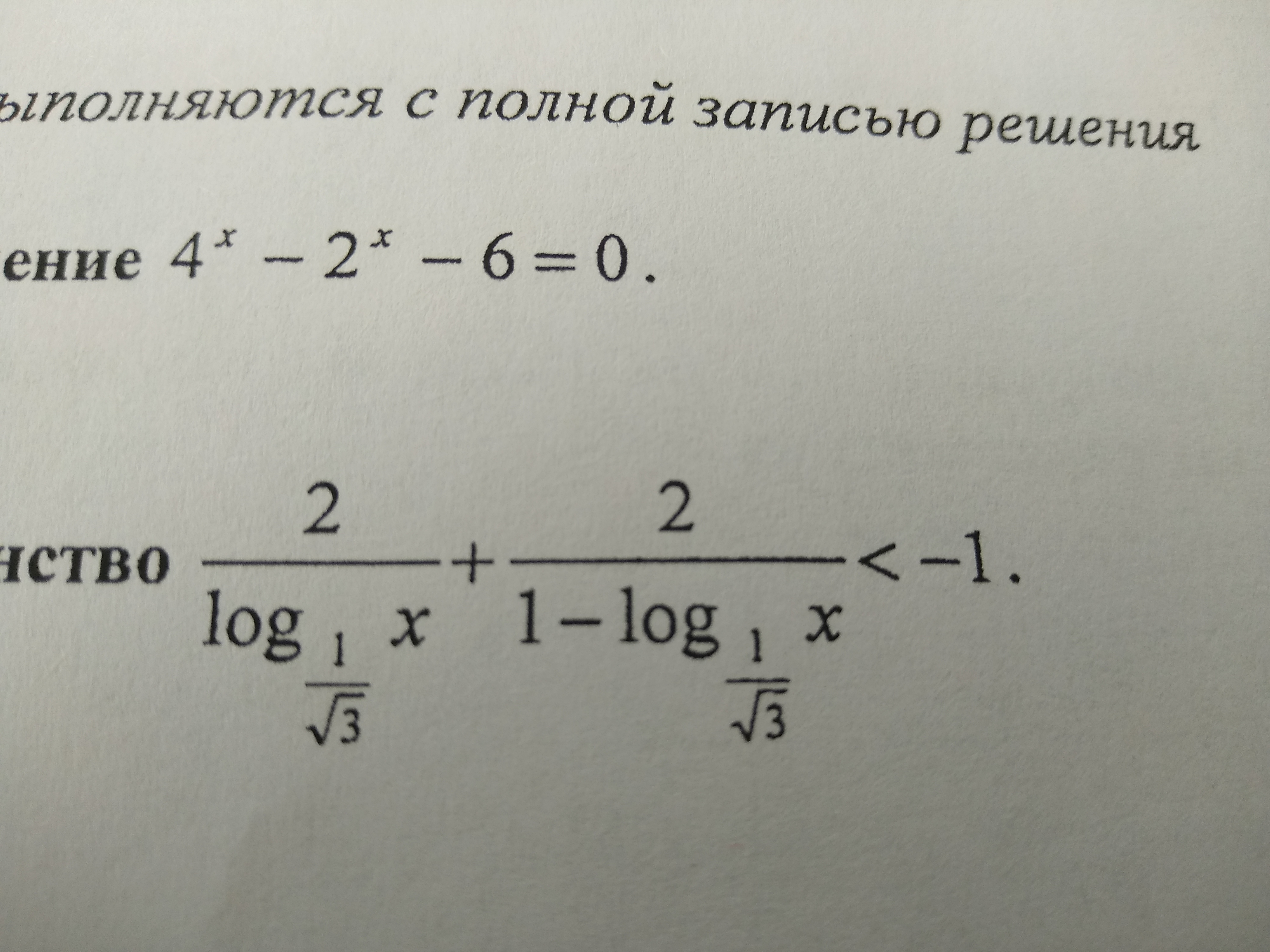
Ответы
Автор ответа:
0
Графическая модель решения неравенства - во вложении.
Из рисунка следует: -1 < t < 0. Вернемся к х:
Ответ:
Приложения:

Похожие вопросы
Предмет: Алгебра,
автор: torlakg
Предмет: География,
автор: mmoldobaev57
Предмет: Математика,
автор: koyshinamalika
Предмет: Математика,
автор: ngztina
Предмет: Математика,
автор: Аноним