Посчитать сумму:
3*1/2^2+5*(1/2^3+1/2^4)+7*(1/2^4+1/2^5+1/2^6)+...+(2n+1)(1/(2^(n+1))+1/2^(2+n)+...+1/2^(2n-1))
3*x^2+5*(x^3+x^4)+7*(x^4+x^5+x^6)+...+(2n+1)((x^(n+1))+x^(2+n)+...+x^(2n-1))
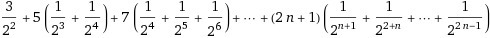
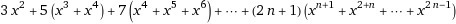
Ответы
Последовательность немного неверно определена, конечное число должно равняется x^(2n) S=3x^2+5(x^3+x^4)+7(x^4+x^5+x^6)+..+(2n+1)(x^(n+1)+x^(n+2)+...+x^(2n))
По сумме геометрической прогрессии
3x^2=3x^2(x-1)/(x-1) 5(x^3+x^4)=5x^3(x^2-1)/(x-1) 7(x^4+x^5+x^6)=7x^4(x^3-1)/(x-1) ....
(2n+1)(x^(n+1)+x^(n+2)+...+x^(2n))=(2n+1)x^(n+1)(x^n-1)/(x-1)
Тогда
S=((3x^3+5x^5+7x^7+...+(2n+1)x^(2n+1))-(3x^2+5x^3+7x^4+9x^5+...+(2n+1)x^(n+1)))/(x-1)
Рассмотрим
A=3x^3+5x^5+7x^7+...+(2n+1)x^(2n+1)
Домножим на x^2 и отняв от A
A-Ax^2 = 3x^3+2(x^5+x^7+x^9+...+x^(2n+1))-(2n+1)x^(2n+3)
То есть получаем геометрическую между двумя членами последовательности, сумма которой равна
x^5+x^7+x^9+...+x^(2n+1)=x^5*(x^(2n-2)-1)(x^2-1)
Значит
A=(3x^3-(2n+1)x^(2n+3)+2x^5(x^(2n-2)-1)/(x^2-1))/(1-x^2)
Аналогично и
B=(3x^2+5x^3+7x^4+9x^5+...+(2n+1)x^(n+1)))/(x-1)
Домножим на x и проделывая те же операции
B=(3x^2-(2n+1)x^(n+2)+2x^3(x^n-1)/(x-1))(1-x)
Значит S=(A-B)/(x-1)
Так как x=1/2 то предел при n->+oo
Получаеться
A при x=1/2 и n->+oo
A=(3*(1/2)^3-2*(1/2)^5/(1/4-1))/(3/4)=11/18
B=(3*(1/2)^2-2*(1/2)^3/(1/2-1))/(1/2) =5/2
S=(11/18-5/2)/(-1/2) = (45-11)/9 =34/9