Предмет: Геометрия,
автор: kugergin07
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ADB равен 30°. Найдите градусную меру угла BAC.
Аноним:
Без рисунка сложно понять
Ответы
Автор ответа:
2
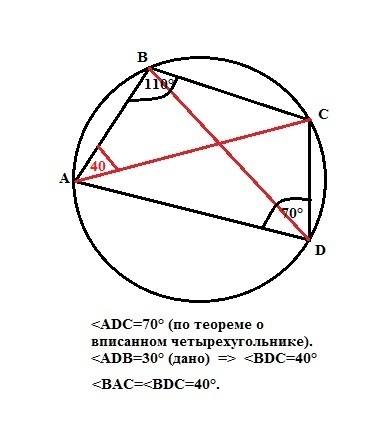
Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°. (Теорема).
Угол ADC четырехугольника - противоположен углу АВС и равен
180 - 110 = 70°.
<ADC =<ADB+<BDC => <BDC=70°-30° = 40°.
Угол BDC вписанный и опирается на дугу ВС, на которую опирается и вписанный угол ВАС. Следовательно, <BAC = 40°.
Ответ: <BAC = 40°.
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ibraevkairat412
Предмет: Математика,
автор: fishanuto4ka
Предмет: Математика,
автор: kutinasona44
Предмет: Биология,
автор: mogoch
Предмет: Математика,
автор: кул7