Предмет: Алгебра,
автор: Аноним
Решите все внятно и понятно, 15б!
Приложения:
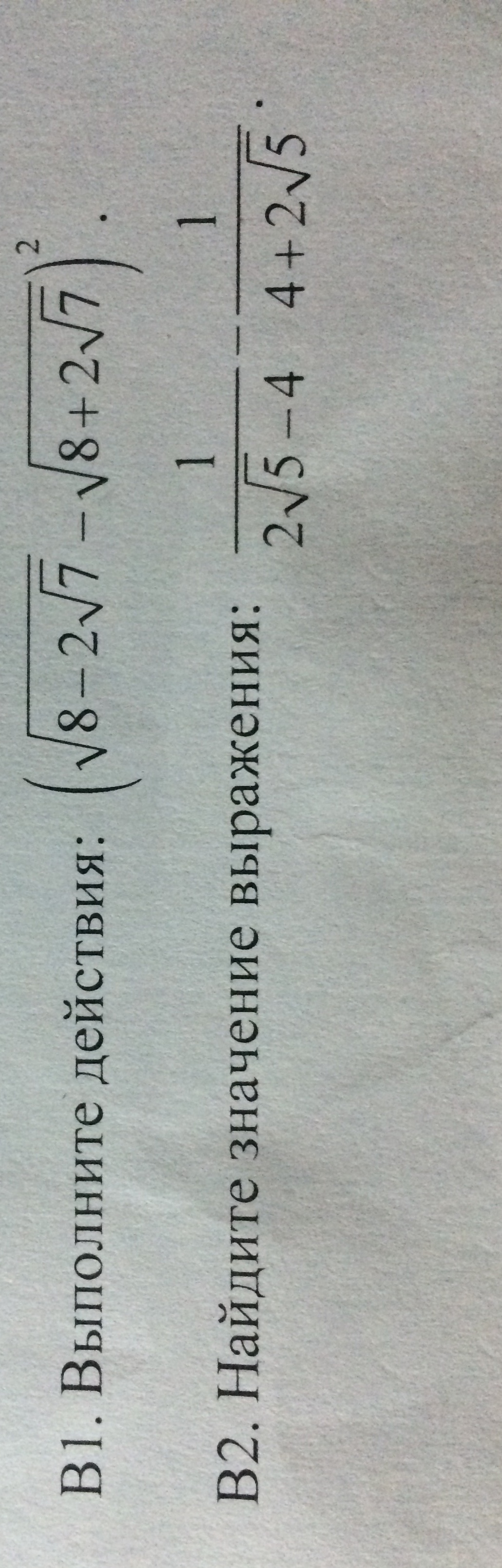
Ответы
Автор ответа:
1
Автор ответа:
0
B1.
B2.
Похожие вопросы
Предмет: Русский язык,
автор: ceerovap
Предмет: Математика,
автор: pilicekaterina
Предмет: Английский язык,
автор: Oookeey
Предмет: Математика,
автор: Taxa28