Предмет: Алгебра,
автор: hjcxd
помогите пожалуйстааа
Приложения:
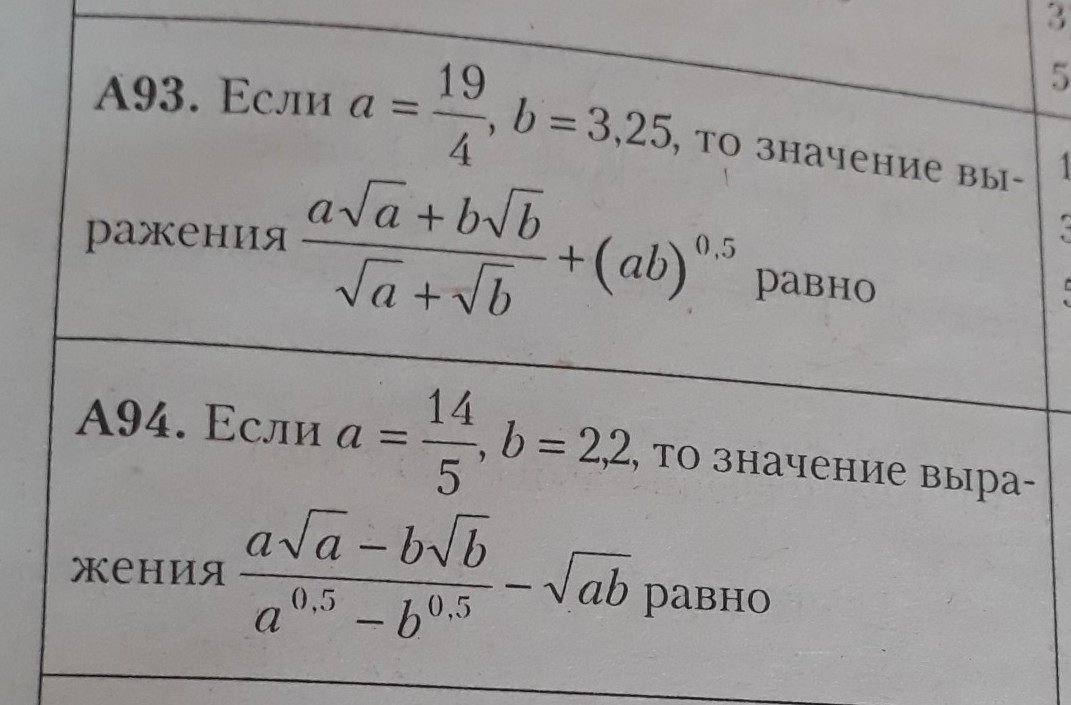
Ответы
Автор ответа:
0
А93 )

А94 )

А94 )
Похожие вопросы
Предмет: Немецкий язык,
автор: Helpak
Предмет: Алгебра,
автор: RomaSayplay
Предмет: Химия,
автор: alpha222333
Предмет: Математика,
автор: niuralagun15
Предмет: Литература,
автор: розочкаалиночка