Предмет: Алгебра,
автор: marafonerro
Известно, что  - углы II четверти и
- углы II четверти и  . Найдите: sin(
. Найдите: sin( )
)
Ответы
Автор ответа:
1
sin(α + β) = sinα*cosβ + sinβ*cosα
cos²α = 1 - sin²α = 1 - (4/5)² = 1 - 16/25 = 9/25
cosα = +- 3/5
но т.к. α ∈ II четверти, где cos < 0, то cosα = -3/5
sin²β = 1 - cos²β = 1 - (-15/17)² = 1 - 225/289 = 64/289
sinβ = +- 8/17,
но т.к. β ∈ II четверти, где sin > 0, то sinβ = 8/17
sin(α + β) = sinα*cosβ + sinβ*cosα = 4/5*(-15/17) + 8/17*(-3/5) = -60/85 - 24/85 = -84/85
Автор ответа:
2
_______________________
ОТВЕТ: - 84/85
ОТВЕТ: - 84/85
Приложения:
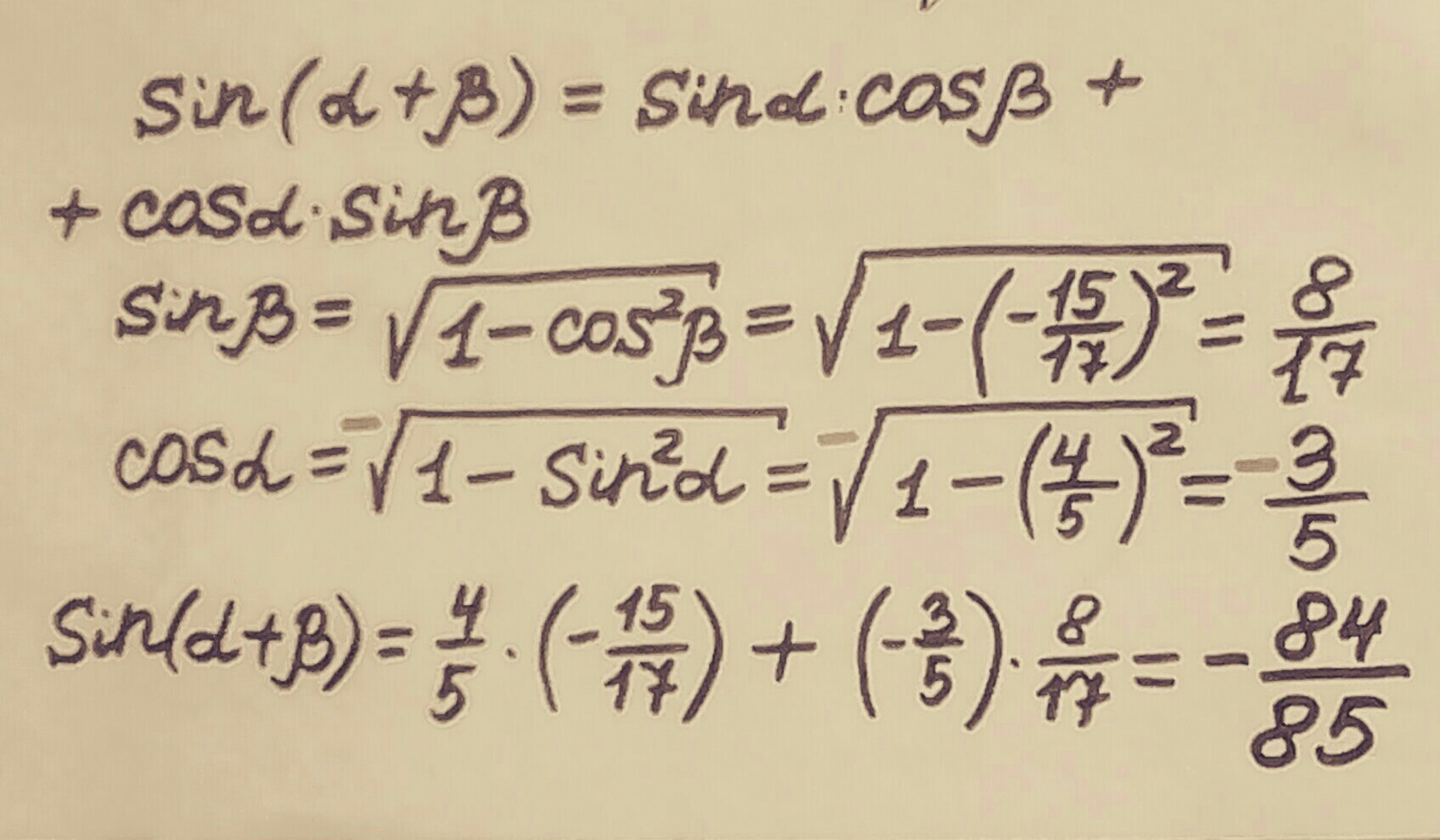
Похожие вопросы
Предмет: Алгебра,
автор: kimjen08
Предмет: Алгебра,
автор: ulyana3714
Предмет: Биология,
автор: ira87052056769
Предмет: Математика,
автор: beznogova2013