Question

В равнобедренном треугольнике АВС основание АС равен 10 см CD биссектриса и угол АСD равен углу АВС . Найдите СD.

Answer 1

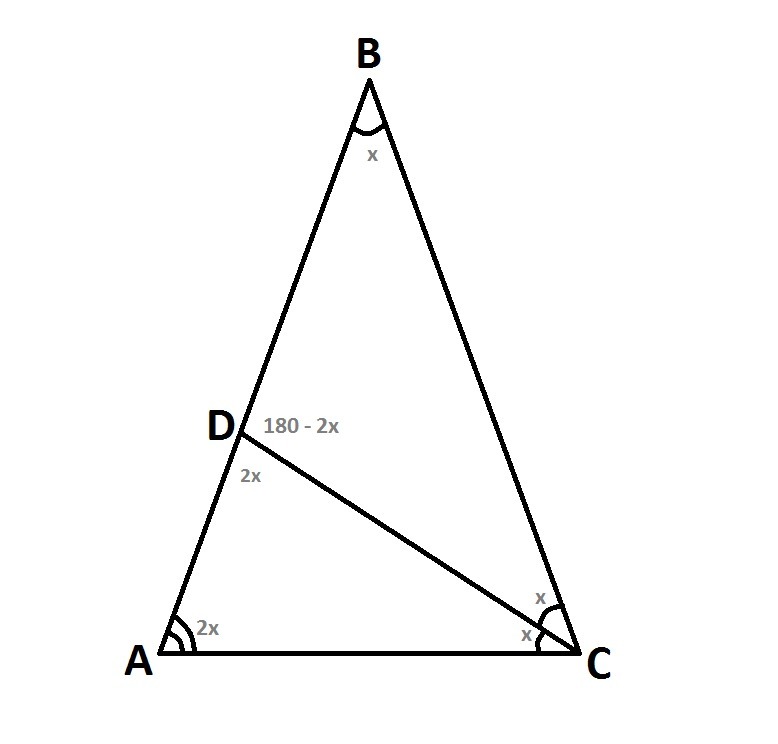
Пусть угол ACD равен x. По условию сказано, что угол ABC равен углу ACD, значит угол ABC равен x. Так как CD биссектриса, значит угол DCB равен углу ACD и равен x. По теореме об углах треугольника, угол BDC в треугольнике CDB равен 180 - x - x = 180 - 2x. По теореме о смежных углах, угол ADC равен 180 - (180 - 2x) = 180 - 180 + 2x = 2x. Так как треугольник ABC равнобедренный, угол BAC равен углу ACB (угол ACB = угол ACD + угол DCB = 2x). Получается, что угол BAC равен 2x. Так как угол BAC равен 2x, и угол ADC равен 2x, понятно что треугольник ADC равнобедренный (углы при основе равны). Следовательно AC = CD = 10 см. Ответ: биссектриса CD равна 10 см.