Предмет: Математика,
автор: kiselevaarina2p0sp6z
ПОЖАЛУЙСТА! ПОМОГИТЕ , ОБЪЯСНИТЕ КАК РЕШАТЬ, БУДУ БЛАГОДАРНА)))))))
Приложения:
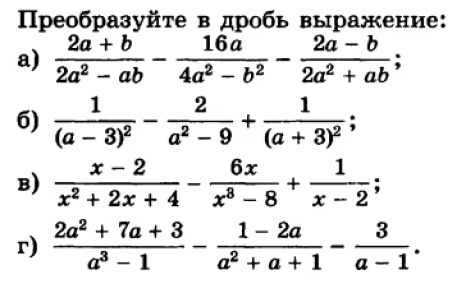
Ответы
Автор ответа:
1
а)

б)

в)

г)

Всё это легко решается, если знать и видеть формулы сокращенного умножения.
б)
в)
г)
Всё это легко решается, если знать и видеть формулы сокращенного умножения.
Похожие вопросы
Предмет: Английский язык,
автор: kiiigiti
Предмет: Қазақ тiлi,
автор: Lqao123
Предмет: Математика,
автор: llllliiiinnnaaa
Предмет: Математика,
автор: rererka