Предмет: Алгебра,
автор: bublik2311
Помогите, пожалуйста
Решить систему:
2х^2+3ху+у^2=0
х^2-ху-у^2=4
Приложения:
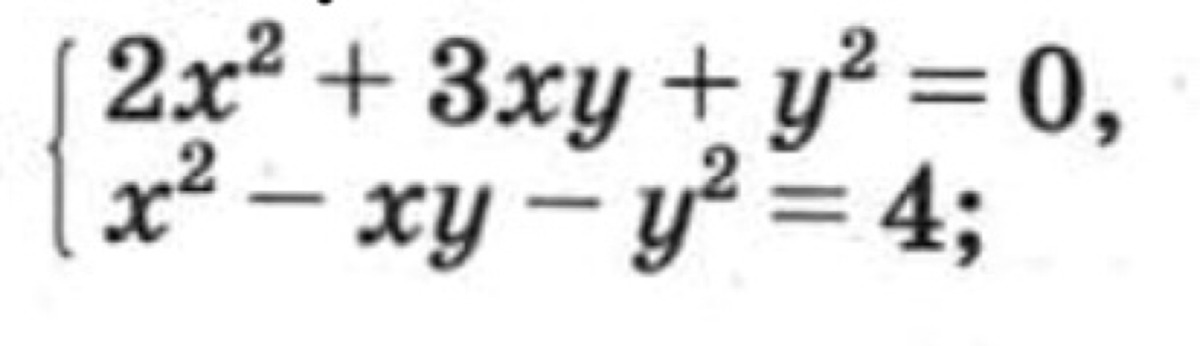
Ответы
Автор ответа:
2
Пара чисел х=0, у=0 не удовлетворяет второму уравнению системы, следовательно, не является решением системы уравнений. Поэтому разделим первое уравнение системы на у²:
Пусть , тогда 2t²+3t+1=0
t=-1 или t=-0,5
Получим 2 случая продолжения решения исходной системы.
В этом случае решений нет, т.к. уравнение х²=-4 не имеет корней.
Ответ: (-2; 2); (2; -2).
Приложения:

Похожие вопросы
Предмет: Математика,
автор: aneltuylegen
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: amirzankanatkanuly
Предмет: Алгебра,
автор: Tasha3333333