Предмет: Алгебра,
автор: hgfd
Расписать решение
1.Решить уравнение(выбрать корни)
2.Решить неравенство
Приложения:
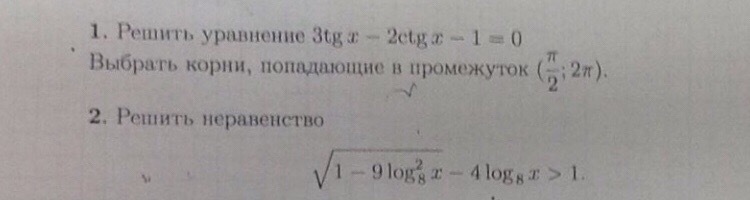
Ответы
Автор ответа:
0
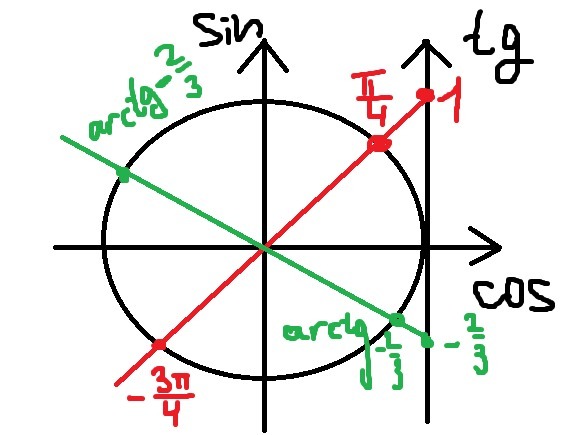
Ответ: a) π/4 + πn, n ∈ Z, arctg(-2/3) + \pi k, k \in Z
b) 5π/4, arctg(-2/3) + π/2, arctg(-2/3) + 3π/2
Решим уравнение:
ИЛИ
Пересечём (2) и (3):
Пересечём (2) и (3) с (3) и (4):
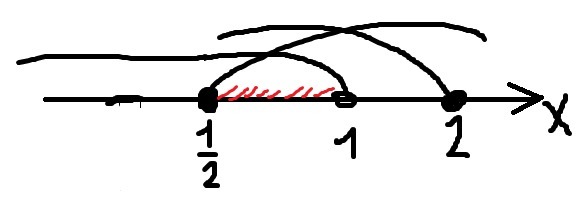
Учтём ОДЗ (рисунок 3):
Ответ: x ∈ [1/2; 1)
Приложения:

Похожие вопросы
Предмет: Математика,
автор: testakk20192019
Предмет: Алгебра,
автор: xxxlllko888
Предмет: Русский язык,
автор: yanafoks
Предмет: Алгебра,
автор: юлия1105
Предмет: История,
автор: strezi82