Предмет: Алгебра,
автор: Muxacekakbar
Объясните, пожалуйста, как раскрылась эта сумма!) <3
Приложения:
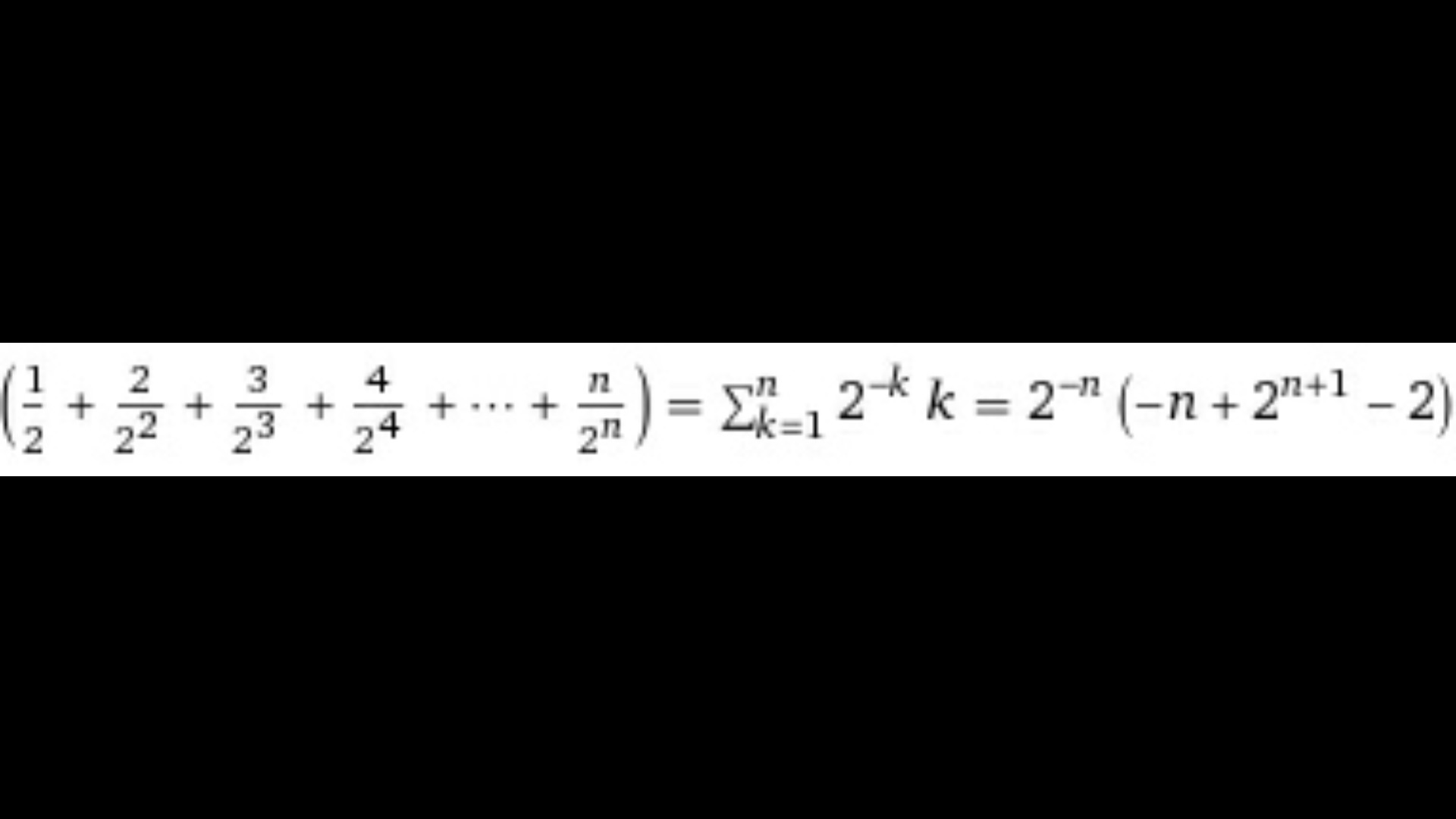
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: kiiigiti
Предмет: Другие предметы,
автор: Аноним
Предмет: Информатика,
автор: user4812789431
Предмет: Математика,
автор: ДинКейт