Предмет: Алгебра,
автор: TMuhriddin
Нужна помощь с задачей номер 7
Приложения:
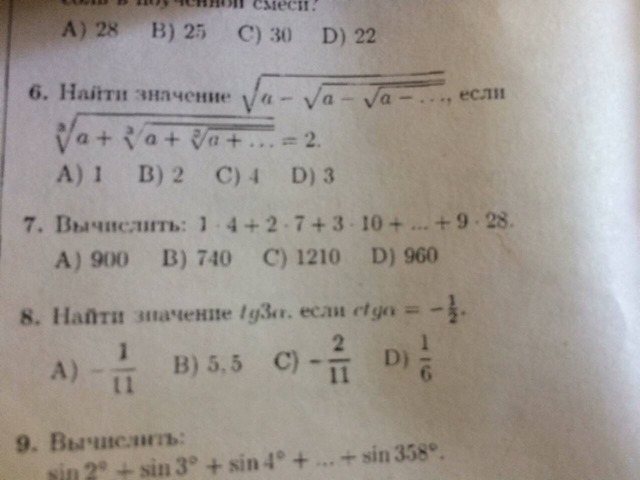
Ответы
Автор ответа:
1
Пусть n – произвольное натуральное число. Тогда справедлива следующая формула, которая называется конечной числовой суммой:
Эта формула доказывается непосредственно методом математической индукции.
Аноним:
Сейчас проверять буду)
Нашел, сейчас поправлю
Пожалуйста дайте ссылку на литературу по этой теме
Похожие вопросы
Предмет: Математика,
автор: dilnaz2010n
Предмет: Математика,
автор: Аноним
Предмет: Другие предметы,
автор: MOLYA2010
Предмет: Химия,
автор: Vikish123
Предмет: Математика,
автор: chelovechek228