У відповідь записати суму всіх цілих чисел які не є розвязками нерівності
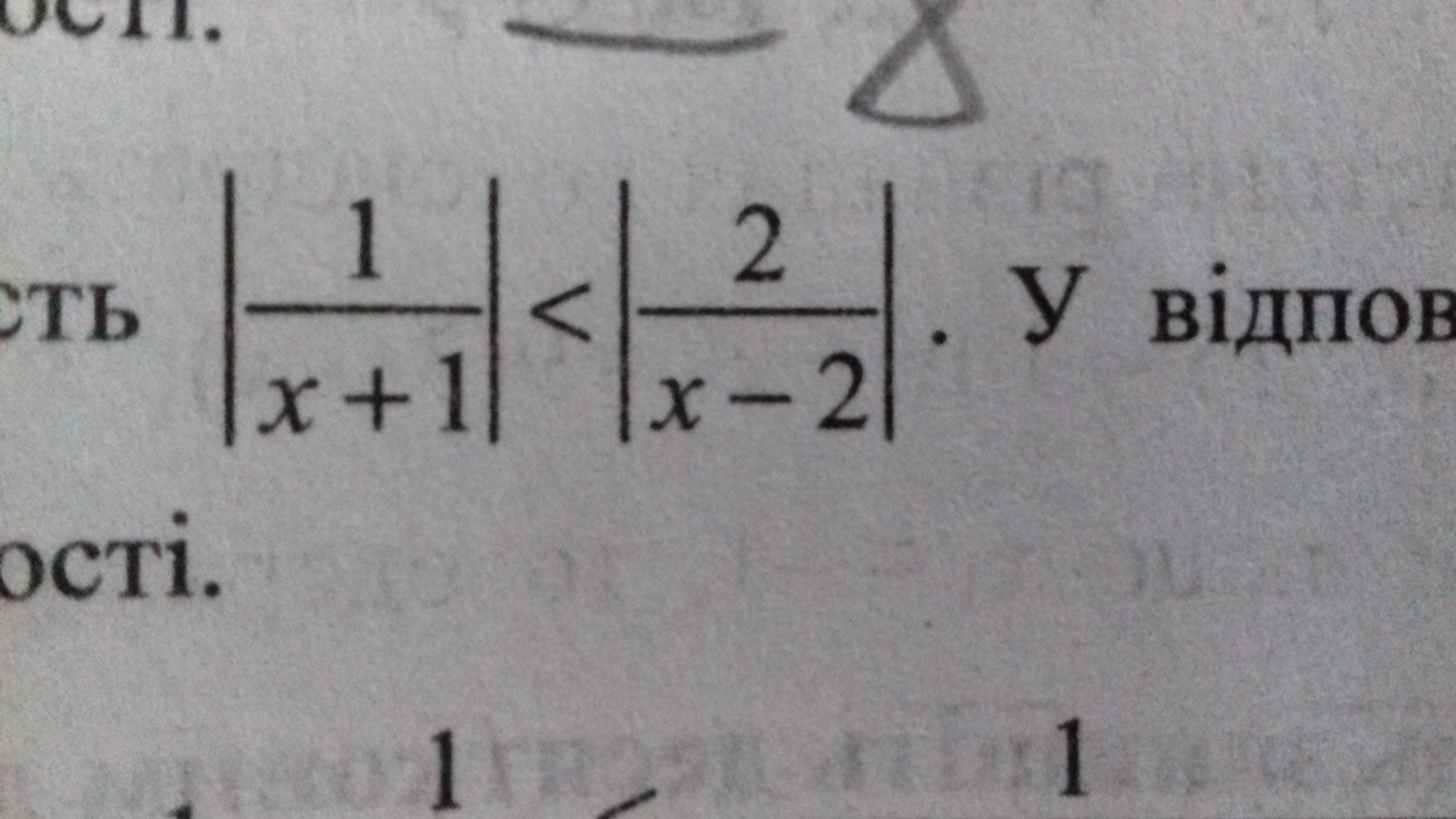
Ответы
|1/(x+1)|<|2/(x-2)|
ОДЗ: x+1≠0 x≠-1 x*-2≠0 x≠2 ⇒
-∞___________-1___________2___________+∞
x∈(-∞;-1)
-(1/(x+1)<-(2/x-2) |×(-1)
1/x+1>2/(x-2)
1/(x+1)-2/(x-2)>0
(x-2-2*(x+1)/((x+1)(x-2))>0
(x-2-2x-2)/((x+1)(x-2))>0
(-x-4)//((x+1)(x-2))>0 |×(-1)
(x+4)/((x+1)(x-2))<0
-∞_____-______-4______+_____-1______-______2______+______+∞ ⇒
x∈(-∞;-4).
x∈(-1;2)
1/(x+1)<-2/(x-2)
1/(x+1)+2/(x-2)<0
(x-2+2*(x+1)/((x+1)(x-2))<0
(x-2+2x+2)/((x+1)(x-2))<0
3x/((x+1)(x-2))<0
-∞____-____-1____+____0____-____2_____+_____+∞ ⇒
x∈(0;2).
x∈(2;+∞)
1/(x+1)<2/(x-2)
1/(x+1)-2/(x-2)<0
(x-2-2*(x+1)/((x+1)(x-2))<0
(x-2-2x-2)/((x+1)(x-2))<0
(-x-4)/((x+1)(x-2))<0 |×(-1)
(x+4)/((x+1)(x-2))>0
-∞____-____-4____+____-1_____-____2____+_____+∞ ⇒
x∈(2;+∞) ⇒
x∈(-∞;-4)U(0;2)U(2;+∞) ⇒
x∉[-4;0]U[2] ⇒
∑=-4+(-3)+(-2)+(-1)+0+2=-8.
Ответ: -8.