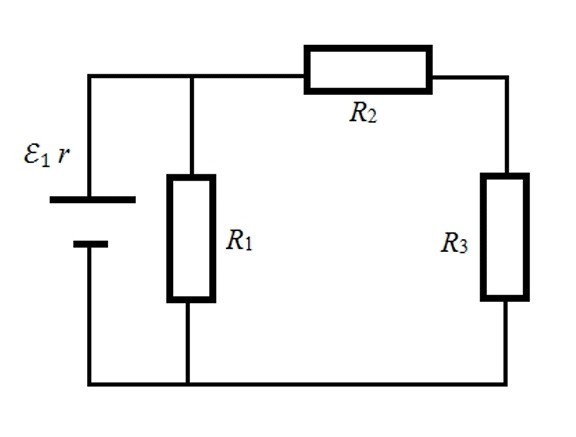
Определите напряжение на резисторе R3 в электрической цепи, схема которой приведена на рисунке. Параметры цепи: r = 1.01 Ом, R1 = 0.4Ом, R2 = 1.0 Ом, R3 = 3.0 Ом, E = 6B.
Ответы
Наиболее простым вариантом будет найти ток через R3, воспользовавшись методом эквивалентного сопротивления (легче было бы воспользоваться I и II законами Кирхгофа, но этот способ более трудоемкий в плане объяснения и понимания).
Сущность метода эквивалентного сопротивления заключается в следующем: представить сопротивления в схеме в виде одного эквивалентного сопротивления (цепь как бы сворачивается), найти ток в неразветвленной части цепи и затем использовать эти данные для нахождения всех остальных необходимых токов (цепь как бы разворачивается).
Найдем сопротивление R23, эквивалентное сопротивлениям R2 и R3:
R2 и R3 соединены последовательно, поэтому
R23 = R2+R3 = 1+3 = 4 Ом
Теперь сопротивления R23 и R1 соединены параллельно, значит
R123 = (1/R1+1/R23)^-1 = (1/0.4+1/4)^-1 = 0.3636 Ом
Сопротивление R123 соединено последовательно с внутренним сопротивлением источника ЭДС, таким образом
Rэ = r+R123 = 1.01+0.3636 = 1.3736 Ом
По закону Ома найдем общий ток цепи:
I = E/Rэ = 6/1.3736 = 4.368 А
Падение напряжения на внутреннем сопротивлении:
Ur = I*r = 4.368*1.01 = 4.4116 В
Таким образом, к R2 и R3 вместе приложено напряжение
U23 = E-Ur = 6-4.4116 = 1.5884 В
Таким образом, ток через резистор R3 (и R2, так как через них течет один и тот же ток):
I23 = U23/R23 = 1.5884/4 = 0.3971 А
И, наконец, найдем падение напряжения на R3:
U3 = I23*R3 = 0.3971*3 = 1.1913 В
Послед. R23=1+3=4 Ом, паралл. R123=(0.4*4)/(0.4+4)= 0.4/1.1=, общее R=1.01+0.4/1.1=1.511/1.1= , ток I=E/R =6*1.1/1.511=6.6/1.511= , напряжение источника U=E-I*R=6-6.6/1.511= , ток через R2, R3 I23=U/R23=U/4= , напряжение U3=I23*R3=U*3/4 = -калькулятор ответит