Предмет: Алгебра,
автор: sasha2278
помогите пожалуйста
Приложения:
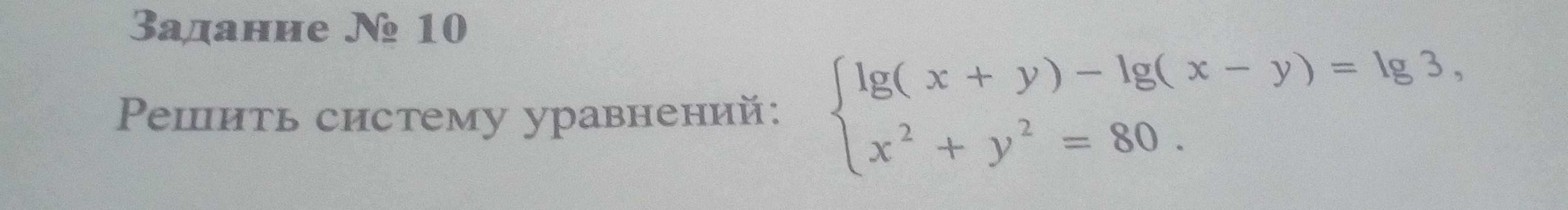
Ответы
Автор ответа:
0
или
Для первой системы не выполняются неравенства. Значит, только пара х=8, у=4 является решением исходной системы уравнений.
Ответ: (8; 4).
Приложения:

Похожие вопросы
Предмет: Українська мова,
автор: zepetohouse24
Предмет: Химия,
автор: kairatulyermakan8
Предмет: Русский язык,
автор: sabinaomarova06
Предмет: Математика,
автор: eltax555
Предмет: История,
автор: Ksenia100500