Предмет: Алгебра,
автор: gan1466
найти модуль суммы корней уравнения log2x^2-1 (x+2)=1/2
где 2x^2 -1 основание числа (x+2)
Ответы
Автор ответа:
1
ОДЗ:
не удовлетворяет ОДЗ.
Корень один х = 5
LFP:
ОДЗ неточное... основание логарифма тоже содержит икс...
если проверить то все сходится
что сходится? основание логарифма не может быть равно 1...
я бы хотел увидеть твоё решение.
Автор ответа:
0
решение такое же, что и у первого автора...
ответ другой...
Ответ: 5
Приложения:
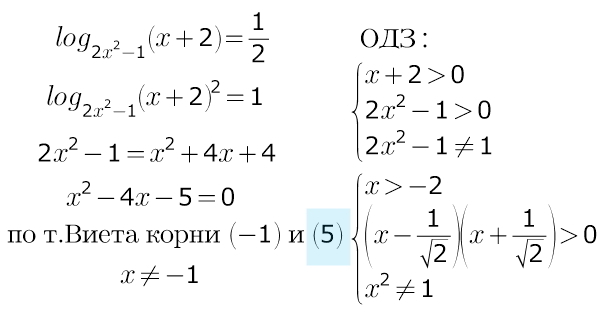
в задании. написано что нужно найти сумму корней выражения
(-1) корнем НЕ является...
в задании написано про модуль суммы (я читала))
хорошо наэтом и сойдемся, что -1 не является корнем.
Похожие вопросы
Предмет: Литература,
автор: shimanskayasonya
Предмет: Физкультура и спорт,
автор: raziasmadin113
Предмет: Алгебра,
автор: shadowcat5082
Предмет: География,
автор: Аля098765432
Предмет: Математика,
автор: Вопрос1100