Предмет: Математика,
автор: pechnic
В трапеции с основаниями 3 и 4 диагональ имеет длину 6 и является биссектрисой одного из углов. Площадь трапеции, умноженная на √ 112 равна…
Ответы
Автор ответа:
0
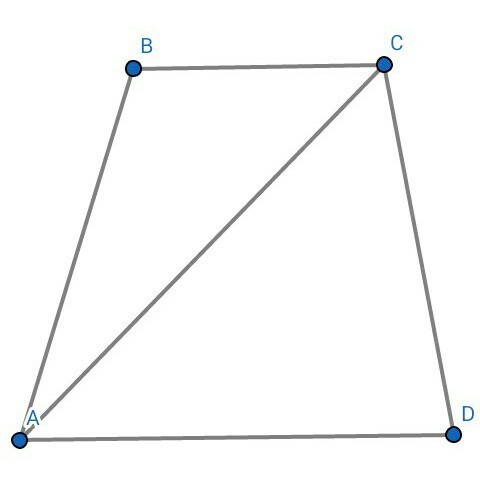
ДАНО: АВСD - трапеция , ВС = 3 см , АD = 4 cм , АС = 6 см , угол АСВ = угол АСD ( или угол ВАС = угол САD )
НАЙТИ: S abcd × √112
_____________________________
РЕШЕНИЕ:
A) 1 случай, когда угол ВАС = угол CAD
угол САD = угол АСВ - как накрест лежащие углы при параллельных прямых ВС и AD и секущей АС
Значит, АВС - равнобедренный => AB = BC = 3 cm
Рассмотрим ∆ АВС :
По свойству треугольника : каждая из сторон треугольника меньше суммы двух других сторон. Проверим это
АВ < ВС + АС
3 < 3 + 6
3 < 9 - верно
АС < ВС + АВ
6 < 3 + 3
6 < 6 - не верно
Значит, треугольника со сторонами 3 , 3 , 6 не существует
Поэтому угол ВАС ≠ угол САD
Б ) 2 случай, когда угол АСВ = угол АСD
угол ACB = угол CAD - как накрест лежащие углы при параллельных прямых ВС и AD и секущей AC
Значит, CAD - равнобедренный => CD = AD = 4 cm
Рассмотрим ∆ АВС :
Также проверим на свойство треугольника
АС < АD + CD
6 < 4 + 4
6 < 8 - верно
AD < AC + CD
4 < 6 + 4
4 < 10 - верно
CD < AD + AC
4 < 4 + 6
4 < 10 - верно
Значит, треугольник со сторонами 4 , 4 , 6 существует
Поэтому угол ACB = угол ACD
B) Рассмотрим ∆ АСD :
Пусть угол САD = a, тогда
По теореме косинусов:
CD² = АD² + AC² - 2× AD × AC × cosa
4² = 4² + 6² - 2×4×6× cosa
16 = 16 + 36 - 48cosa
cosa = 36/48 = 3/4
Г) Рассмотрим ∆ АВС:
угол АСВ = угол САД = а
По теореме косинусов:
AB² = BC² + AC² - 2 × BC × AC × cosa
AB² = 3² + 6² - 2×3×6 × ( 3/4 )
AB² = 9 + 36 - 27 = 18
AB = 3√2 cm
Д) Рассмотрим ∆ САD :
По формуле Герона:
Где a, b, c - cтороны треугольника
р = ( a + b + c )/2 - полупериметр
S cad =
S cad = 3√7 cm²
E ) Рассмотрим ∆ АВС :
По формуле Герона :
S abc =
S abc = 9/4 × √7 cm²
S abcd × √112 = ( S abc + S cad ) × √112 =
ОТВЕТ: 147 см²
Приложения:
Похожие вопросы
Предмет: Литература,
автор: aaaaanegroideker
Предмет: Литература,
автор: kapystaVlada
Предмет: Математика,
автор: selenko72
Предмет: География,
автор: юльча20