Предмет: Алгебра,
автор: dyubko
Найдите, при каких значениях a и b многочлен х⁴+6х³+3х²+ax+b делится без остатка на многочлен x²+4x+3
Ответы
Автор ответа:
11
Решение задачи на фото ниже
Приложения:
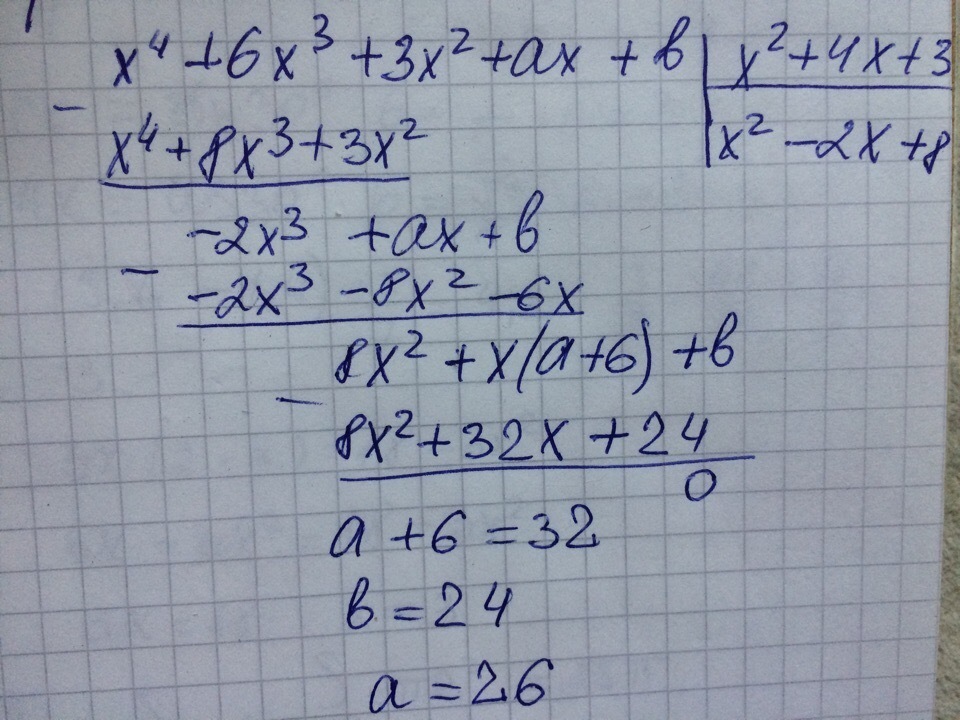
Автор ответа:
6
Получаем, что x^2+4x+3 имеет корни -3 -1 (по теореме Виета)
Значит можем представить наш многочлен как (x+3)(x+1)
Так как многочлен 4 степени делится на наш многочлен 2 степени, то справедлива запись:
x^4+6x^3+3x^2+ax+b = (x+3)(x+1)Q(x).
Теперь подставим вместо x = -3, получим(1 уравнение), x = -1(второе уравнение)
1) 81-162+27-3a+b = 0
2) 1-6+3-a+b = 0
Нужно решить данную систему.
b-3a=54
b-a=2. (вычтем из 2 уравнения первое)
2a= -52 a = -26
Тогда b = -24
Ответ: a = -26 b =-24
Похожие вопросы
Предмет: Українська мова,
автор: sonickakolisnyk
Предмет: Литература,
автор: nnoskov35
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: L1tePool