Предмет: Геометрия,
автор: TMuhriddin
Нужна помощь с задачей номер 23
Приложения:

NeZeRAvix:
у меня 20 получается
Да тут есть опечатки
Ответы
Автор ответа:
1
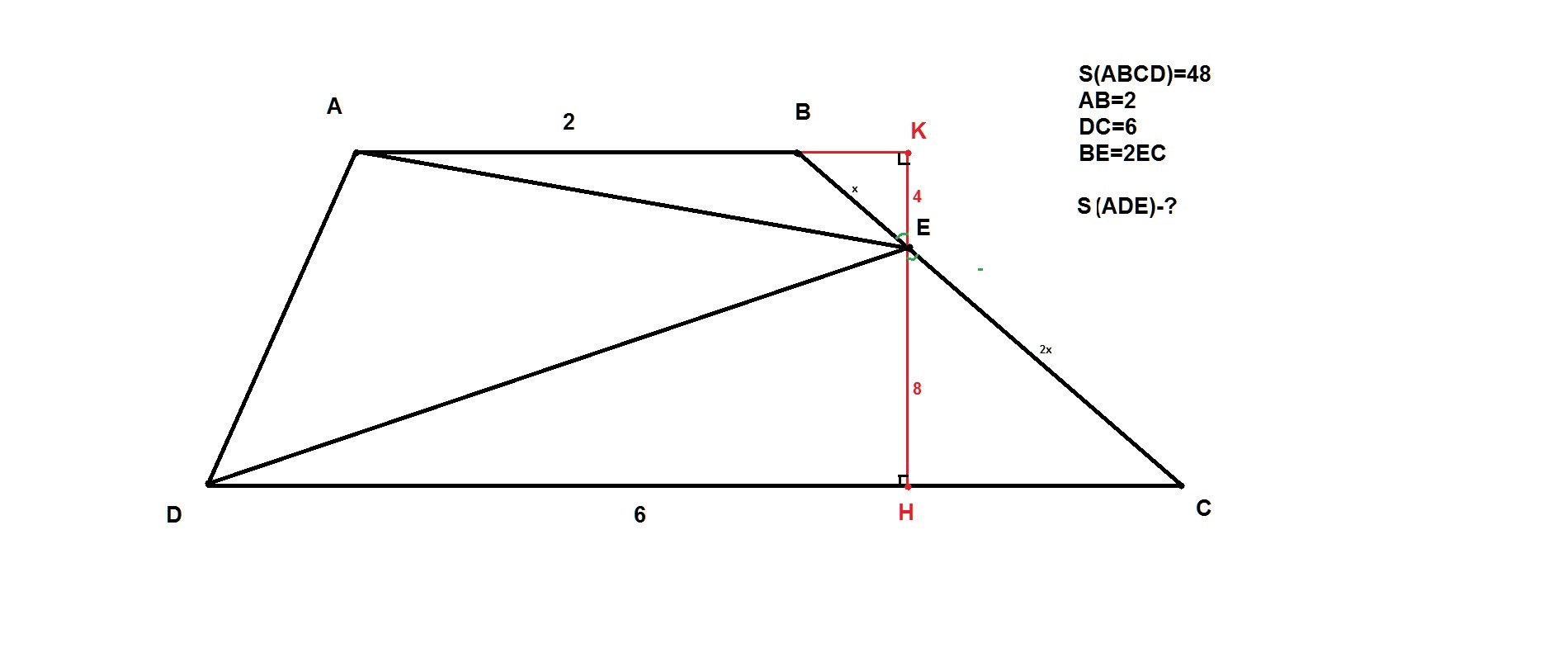
Найдем площади треугольников ABE и DEC, а затем вычтем их из площади всей трапеции и получим нужную нам площадь ADE.
Сразу делаем доп. построения: проводим высоту трапеции KH через точку E.
Из площади трапеции:
значит KH=12
Рассмотрим треугольники BKE и EHC: они подобны по двум углам:
1) ∠BEK=∠HEC как вертикальные
2) ∠BKE=∠EHC=90° (т.к. KH - высота)
отсюда:
KE и EH - высоты треугольников ABE и DEC соответственно.
Площадь треугольника равна половине произведения его высоты на основание:
значит
Ответ: 20
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: msusko12
Предмет: Английский язык,
автор: Аноним
Предмет: Экономика,
автор: zefirka2009
Предмет: Алгебра,
автор: 90008009
Предмет: Математика,
автор: Биологичка9988