Предмет: Алгебра,
автор: GrishenkaMilenov
Помогите решить, пожалуйста. :)
Приложения:
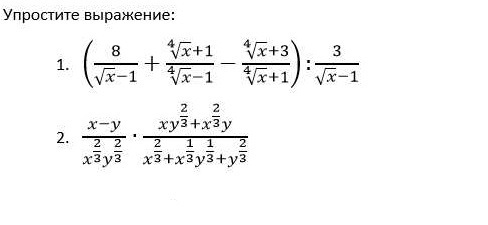
Ответы
Автор ответа:
0
1.
![( \frac{8}{ \sqrt{x} - 1 } + \frac{ \sqrt[4]{x} + 1}{ \sqrt[4]{x} - 1} - \frac{ \sqrt[4]{x} + 3}{ \sqrt[4]{x} + 1} ) \div \frac{3}{ \sqrt{x} - 1} = ( \frac{8}{( \sqrt[4]{x} - 1)( \sqrt[4]{x} + 1) } + \frac{ {( \sqrt[4]{x} + 1)}^{2} }{( \sqrt[4]{x} - 1)( \sqrt[4]{x} + 1)} - \frac{( \sqrt[4]{x} + 3)( \sqrt[4]{x} - 1) }{ (\sqrt[4]{x} - 1)( \sqrt[4]{x} + 1)} \div \frac{3}{ \sqrt{x} - 1} = ( \frac{8 + \sqrt{x} + 2 \sqrt[4]{x} + 1 - \sqrt{x} - 3 \sqrt[4]{x} + \sqrt[4]{x} + 3}{( \sqrt[4]{x} - 1)( \sqrt[4]{x} + 1) } ) \times \frac{ \sqrt{x} - 1}{3} = \frac{12}{ \sqrt{x} - 1} \times \frac{ \sqrt{x} - 1}{3} = 4 ( \frac{8}{ \sqrt{x} - 1 } + \frac{ \sqrt[4]{x} + 1}{ \sqrt[4]{x} - 1} - \frac{ \sqrt[4]{x} + 3}{ \sqrt[4]{x} + 1} ) \div \frac{3}{ \sqrt{x} - 1} = ( \frac{8}{( \sqrt[4]{x} - 1)( \sqrt[4]{x} + 1) } + \frac{ {( \sqrt[4]{x} + 1)}^{2} }{( \sqrt[4]{x} - 1)( \sqrt[4]{x} + 1)} - \frac{( \sqrt[4]{x} + 3)( \sqrt[4]{x} - 1) }{ (\sqrt[4]{x} - 1)( \sqrt[4]{x} + 1)} \div \frac{3}{ \sqrt{x} - 1} = ( \frac{8 + \sqrt{x} + 2 \sqrt[4]{x} + 1 - \sqrt{x} - 3 \sqrt[4]{x} + \sqrt[4]{x} + 3}{( \sqrt[4]{x} - 1)( \sqrt[4]{x} + 1) } ) \times \frac{ \sqrt{x} - 1}{3} = \frac{12}{ \sqrt{x} - 1} \times \frac{ \sqrt{x} - 1}{3} = 4](https://tex.z-dn.net/?f=%28+%5Cfrac%7B8%7D%7B+%5Csqrt%7Bx%7D+-+1+%7D++%2B++%5Cfrac%7B+%5Csqrt%5B4%5D%7Bx%7D++%2B+1%7D%7B+%5Csqrt%5B4%5D%7Bx%7D++-+1%7D++-++%5Cfrac%7B+%5Csqrt%5B4%5D%7Bx%7D++%2B+3%7D%7B+%5Csqrt%5B4%5D%7Bx%7D++%2B+1%7D+%29+%5Cdiv++%5Cfrac%7B3%7D%7B+%5Csqrt%7Bx%7D++-+1%7D++%3D+%28+%5Cfrac%7B8%7D%7B%28++%5Csqrt%5B4%5D%7Bx%7D+++-+1%29%28+%5Csqrt%5B4%5D%7Bx%7D+%2B+1%29+%7D++%2B++%5Cfrac%7B+%7B%28+%5Csqrt%5B4%5D%7Bx%7D++%2B+1%29%7D%5E%7B2%7D+%7D%7B%28+%5Csqrt%5B4%5D%7Bx%7D++-+1%29%28+%5Csqrt%5B4%5D%7Bx%7D++%2B+1%29%7D+++-++%5Cfrac%7B%28+%5Csqrt%5B4%5D%7Bx%7D+%2B+3%29%28+%5Csqrt%5B4%5D%7Bx%7D++-+1%29+%7D%7B+%28%5Csqrt%5B4%5D%7Bx%7D++-+1%29%28+%5Csqrt%5B4%5D%7Bx%7D++%2B+1%29%7D+++%5Cdiv++%5Cfrac%7B3%7D%7B+%5Csqrt%7Bx%7D++-+1%7D++%3D+%28+%5Cfrac%7B8+%2B++%5Csqrt%7Bx%7D+%2B+2+%5Csqrt%5B4%5D%7Bx%7D+++%2B+1+-++%5Csqrt%7Bx%7D+-+3+%5Csqrt%5B4%5D%7Bx%7D+++%2B++%5Csqrt%5B4%5D%7Bx%7D++%2B+3%7D%7B%28+%5Csqrt%5B4%5D%7Bx%7D+-+1%29%28+%5Csqrt%5B4%5D%7Bx%7D++%2B+1%29+%7D++%29+%5Ctimes++%5Cfrac%7B+%5Csqrt%7Bx%7D++-+1%7D%7B3%7D++%3D++%5Cfrac%7B12%7D%7B+%5Csqrt%7Bx%7D++-+1%7D++%5Ctimes++%5Cfrac%7B+%5Csqrt%7Bx%7D++-+1%7D%7B3%7D++%3D+4)
2.

2.
Похожие вопросы
Предмет: Геометрия,
автор: akutagawarun
Предмет: Алгебра,
автор: revalorise29
Предмет: История,
автор: Kanadavimax
Предмет: Математика,
автор: pelexovich