Предмет: Математика,
автор: tanyatreo
Вычислить двойной интеграл,ограниченного заданными линиями: ∫ ∫
D
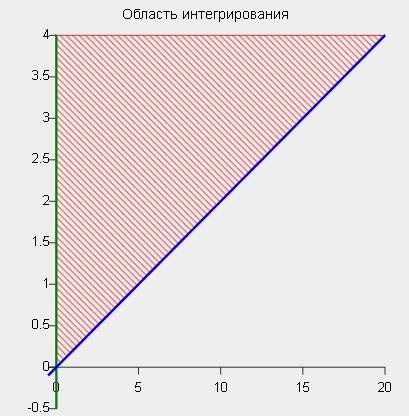
5y^2cos (xy/2)dxdy, если область D ограничена линиями D:x=0, y=4, y=x/5
Аноним:
Ответ то есть?
2-2cos1000 вышло
2(1-cos40)
Ответы
Автор ответа:
2
Интегрируем функцию на множестве, заданном неравенствами
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: bbektemyr
Предмет: Химия,
автор: sokolenkoekaterina21
Предмет: Английский язык,
автор: ademyaydyn
Предмет: Математика,
автор: исида1
Предмет: Алгебра,
автор: vesnasurgut