Question

знайдіть площу трапеціі авсд якщо іі основи ад=28 см, вс= 11 см, а бічні сторони ав=25 см, сд=26 см

Answer 1

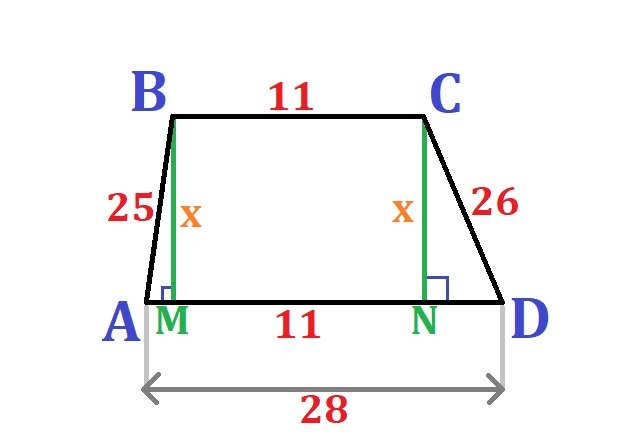
Сделаем небольшой рисунок (см. приложение).

1. Проведём высоты BM, BM ⊥ AD и CN, CN ⊥ AD. Обозначим их длину через "x": BM = CN = x.

2. Рассмотрим треугольник ABM: AM² = 25² - x².

3. Рассмотрим треугольник NCD: ND² = 26² - x².

4. Сторона трапеции AD складывается из трёх частей: AD = AM + MN + ND, где MN = BC = 11 см. Отсюда найдём "x":

$28 = AM + 11 + ND;$

$28 = \sqrt{25^2-x^2} + 11 + \sqrt{26^2 - x^2};$

$17 = \sqrt{25^2-x^2} + \sqrt{26^2 - x^2};$

$289 = 25^2-x^2 + 2\sqrt{25^2-x^2} \sqrt{26^2 - x^2} + 26^2-x^2;$

$2x^2 - 2\sqrt{(25^2-x^2)(26^2 - x^2)} = 25^2 + 26^2 - 289;$

Дальше идёт абсолютно неприемлемое решение "в лоб", потому как других я не увидел.

$2x^2 - 2\sqrt{(25^2-x^2)(26^2 - x^2)} = 625 + 676 - 289;$

$2x^2 - 2\sqrt{(625-x^2)(676 - x^2)} = 1012;$

$x^2 - \sqrt{(625-x^2)(676 - x^2)} = 506;$

$x^2 - 506 = \sqrt{(625-x^2)(676 - x^2)};$

$x^4 - 1012x^2 + 506^2 = (625-x^2)(676 - x^2);$

$x^4 - 1012x^2 + 256036 = x^4 - 1301x^2 + 422500;$

$289x^2 = 166464;$

$x^2 = 576;$

$x = 24.$ (корень -24 нам не подходит)

5. $S = \frac{11+28}{2}*24 = 468$ (см²).

Ответ: 468 см².