Предмет: Математика,
автор: SashaKSK
Вычислите пожалуйста
Приложения:
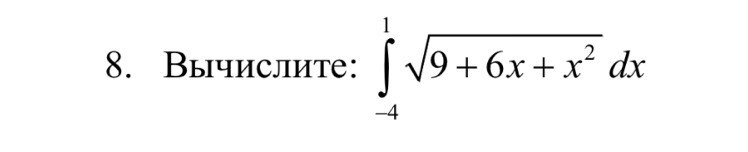
Ответы
Автор ответа:
1
Tricky интеграл, ловите!
Приложения:

Автор ответа:
0
Похожие вопросы
Предмет: Геометрия,
автор: maxcrazy094
Предмет: Физика,
автор: supercatura
Предмет: Математика,
автор: marseltop21
Предмет: География,
автор: KucherM
Предмет: Математика,
автор: Аноним
=∫₋₄¹√((x+3)²)dx=
=∫₋₄¹|x+3|dx
Замена: t=x+3
Пересчитываем пределы интегрирования:
t=-4+3=-1 и t=1+3=4, тогда
∫₋₁⁴|t|dt=
=|∫₋₁⁰tdt|+|∫₀⁴tdt|=
=|t²/2||₋₁⁰+|t²/2||₀⁴=
=|0-1/2|+|8-0|=
=1/2+8=17/2=8,5
Ответ: 8,5.