Предмет: Математика,
автор: Dislokaynt
Не знаю как решить неравенство
Приложения:
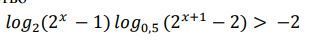
Ответы
Автор ответа:
1
Поскольку этот интервал принадлежит ОДЗ, получаем
Ответ:
Dislokaynt:
Логарифм с основанием 2 в минус первой степени вынес -1 за логарифм и изменил знак? Почему?
Изменил знак только после того, как отбросил минусы в левой и правой части
Похожие вопросы
Предмет: История,
автор: uldasevam01
Предмет: Қазақ тiлi,
автор: gngn24758
Предмет: Қазақ тiлi,
автор: dimasamandyk29
Предмет: Математика,
автор: Sofagreat1234