Предмет: Математика,
автор: Dislokaynt
Не могу найти решение уравнения
Приложения:
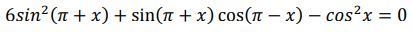
Ответы
Автор ответа:
1
Ответ:
Dislokaynt:
А почему исчезло pi?
И как получились эти тангенсы, я не могу найти такую формулу
1) формулы приведения, 2) делим все уравнение на cos²x
Благодарю, понял
Скажите, а почему деление на косинус не привело к потере решений?
Если cosx=0, то sinx≠0
А значит при cosx=0 уравнение решений не имеет
Все правильно, но мне кажется, это должно быть написано в основном тексте.
Похожие вопросы
Предмет: История,
автор: 5353353434635
Предмет: Алгебра,
автор: Sveta19d87
Предмет: Английский язык,
автор: uldasevaozoda
Предмет: Литература,
автор: alyknysh2005
Предмет: Математика,
автор: николаева5