Предмет: Математика,
автор: нина201826
Помогите решить номер 5, пожалуйста:)
Приложения:
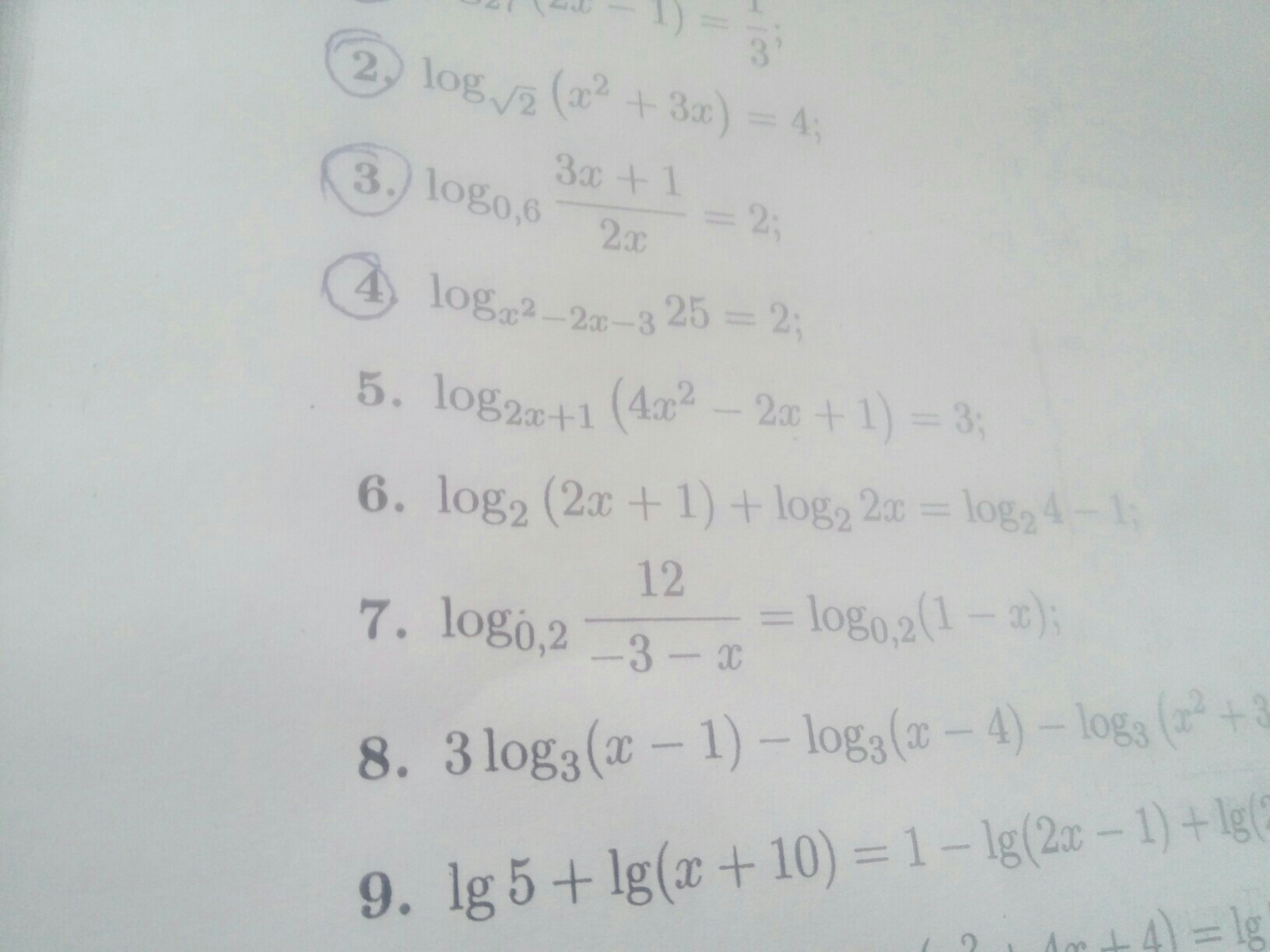
Ответы
Автор ответа:
0
5)

ОДЗ: 2х + 1 > 0
2х + 1 не равно 1
4х^2 - 2х + 1 > 0
D = b^2 - 4ac = 4 - 4*4*1 < 0 => x € R
x > - 1/2
x не равно 0
x € R
=> x € (-1/2; 0) U (0; +беск)

Ответ: нет корней.
ОДЗ: 2х + 1 > 0
2х + 1 не равно 1
4х^2 - 2х + 1 > 0
D = b^2 - 4ac = 4 - 4*4*1 < 0 => x € R
x > - 1/2
x не равно 0
x € R
=> x € (-1/2; 0) U (0; +беск)
Ответ: нет корней.
Автор ответа:
0
lоg(2x+1)(4x²-2x+1)=3
{4x²-2x+1>0;x€R
{2x+1>0;x>-1/2
{2x+1≠1;2x≠0;x≠0
x€(-1/2;0)U(0;+ бес)
это ОДЗ
4x²-2x+1=(2x+1)³
4x²-2x+1=8x³+12x²+6x+1
8x³+12x²+6x+1-4x²+2x-1=0
8x³+8x²+8x=0
8x(x²+x+1)=0
1)x=0 не принадлежит ОДЗ
2)x²+x+1=0
D=1-4=-3<0
x€∅
нет решения
ответ нет решения
{4x²-2x+1>0;x€R
{2x+1>0;x>-1/2
{2x+1≠1;2x≠0;x≠0
x€(-1/2;0)U(0;+ бес)
это ОДЗ
4x²-2x+1=(2x+1)³
4x²-2x+1=8x³+12x²+6x+1
8x³+12x²+6x+1-4x²+2x-1=0
8x³+8x²+8x=0
8x(x²+x+1)=0
1)x=0 не принадлежит ОДЗ
2)x²+x+1=0
D=1-4=-3<0
x€∅
нет решения
ответ нет решения
Похожие вопросы
Предмет: Алгебра,
автор: darabratisko361
Предмет: Математика,
автор: s87075637419
Предмет: Алгебра,
автор: arinasuvorova2709
Предмет: История,
автор: evsikovanadyus
Предмет: Математика,
автор: liana77