Предмет: Геометрия,
автор: missilove002
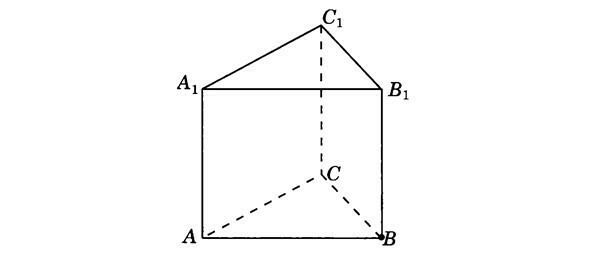
ДАЮ 17 баллов. ПОМОГИТЕ, пожалуйста, решить эту задачу. Точка M1-середина ребра B1C1 правильной треугольной призмы ABCA1B1C1. Найдите косинус угла AM1A1 если боковое ребро BB1 равно 2 корень из 7 а сторона= 4 корень из 3
Ответы
Автор ответа:
8
1) Все боковые ребра правильной треугольной призмы перпендикулярны основаниям.
Так как А1М1 лежит в плоскости А1В1С1, то АА1 перпендикулярно А1М1
Значит, ∆ АА1М1 - прямоугольный
2) Рассмотрим ∆ А1В1С1 ( А1В1 = В1С1 = А1С1 ) :
В равностороннем треугольнике высота равна h = a√3/2
A1M1 = 4√3 × √3/ 2 = 6
AA1 = 2√7
3) Рассмотрим ∆ АА1М1 ( угол АМ1А1 = 90° ):
По т. Пифагора:
АМ1² = АА1² + А1М1²
АМ1² = ( 2√7 )² + 6² = 28 + 36 = 64
АМ1 = 8
сos угол АМ1А1 = А1М1/ АМ1 = 6/8 = 3/4 = 0,75
ОТВЕТ: 0,75
Так как А1М1 лежит в плоскости А1В1С1, то АА1 перпендикулярно А1М1
Значит, ∆ АА1М1 - прямоугольный
2) Рассмотрим ∆ А1В1С1 ( А1В1 = В1С1 = А1С1 ) :
В равностороннем треугольнике высота равна h = a√3/2
A1M1 = 4√3 × √3/ 2 = 6
AA1 = 2√7
3) Рассмотрим ∆ АА1М1 ( угол АМ1А1 = 90° ):
По т. Пифагора:
АМ1² = АА1² + А1М1²
АМ1² = ( 2√7 )² + 6² = 28 + 36 = 64
АМ1 = 8
сos угол АМ1А1 = А1М1/ АМ1 = 6/8 = 3/4 = 0,75
ОТВЕТ: 0,75
Приложения:
Автор ответа:
2
Пусть А - начало координат .
Ось X - AC
Ось Y перпендикулярно Х в сторону В
Ось Z - AA1
Координата точки
М1 ( 3√3; 3; 2√7)
Вектора
М1А ( -3√3;-3;-2√7) длина √(27+9+28)=8
М1А1( -3√3;-3;0) длина √(27+9)=6
Косинус искомого угла
М1А*М1А1/ | М1А| / | М1А1 | = (27+9)/6/8=3/4
Похожие вопросы
Предмет: Литература,
автор: nataliaolgomets
Предмет: Қазақ тiлi,
автор: osmannazarov999
Предмет: Русский язык,
автор: sfjiyeefvnmx
Предмет: Математика,
автор: МАКС20131
Предмет: Биология,
автор: ааа191