Предмет: Математика,
автор: BlackParade
Если кто-то знает, как решить, пожалуйста помогите
Приложения:
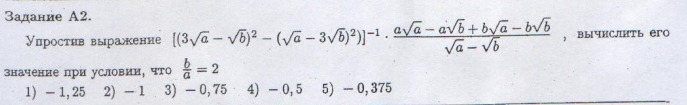
Ответы
Автор ответа:
0
Преобразуем первый множитель
((3√а - √b)² - (√a - 3√b)²)⁻¹ =
=1/(((9а + b - 6√(ab)) - (a + 9b - 6√(ab))) =
=1/(9а + b - 6√(ab) - a - 9b + 6√(ab)) =
1/(8a - 8b) = 1/(8(a - b)
Преобразуем второй множитель
(а√а-а√b + b√a - b√b)/ (√a - √b) =
= (a(√a - √b) + b(√a -√b))/ (√a - √b) =
= (√a - √b)(a + b)/(√a - √b) = a + b
Теперь перемножим результаты преобразования
(1/(8(а - b)) · (a + b) = 0.125(a + b)/(a - b)
и разделим числитель и знаменатель на а
0,125(1 + b/a)/(1 - b/a)
Подставим значение b/a = 2
0.125 (1 + 2)/(1 - 2) = -0.375
Ответ: 5) -0,375
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: icqwko2
Предмет: Геометрия,
автор: kapitonovsergej532
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: георгий47
Предмет: Математика,
автор: дашккак