в прямоугольном параллелепипеде abcda1b1c1d1 ab=2, ad=6, aa1=4. k-середина ad, m-середина bb1, n-середина a1b1. Найти длину перпендикулярной проекции отрезка c1d1 на плоскость kmn
Ответы
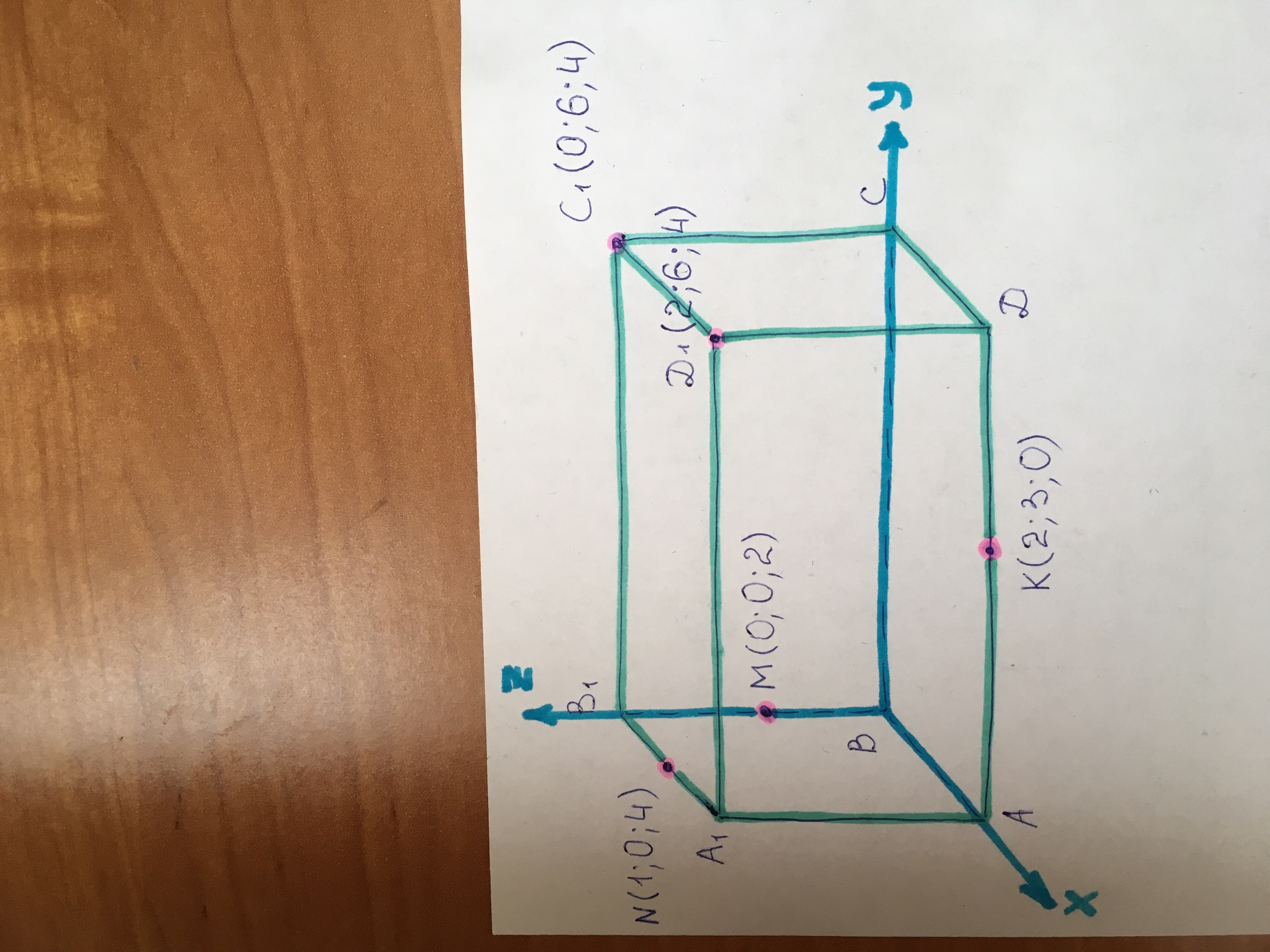
Введём прямоугольную систему координат с началом координат в точке В (см. рис.).
Найдём координат точек:
K (2; 3; 0), M (0; 0; 2), N (1; 0; 4), C₁ (0; 6; 4), D₁ (2; 6; 4).
Найдём уравнение плоскости (KMN):
A(x - 2) + B(y - 3) + Cz = 0
A(0 - 2) + B(0 - 3) + C(2 - 0) = 0
A(1 - 2) + B(0 - 3) + C(4 - 0) = 0
A(x - 2) + B(y - 3) + Cz = 0
-2A - 3B + 2C = 0
-A - 3B + 4C = 0
-A - 3B + 4C = 0
A + 2C = 0
A(x - 2) + B(y - 3) + Cz = 0
A = -2C
2C - 3B + 4C = 0
A(x - 2) + B(y - 3) + Cz = 0
A = -2C
2C - B = 0
A(x - 2) + B(y - 3) + Cz = 0
A = -2C
B = 2C
-2C(x - 2) + 2C(y - 3) + Cz = 0
-2(x - 2) + 2(y - 3) + z = 0
-2x + 4 + 2y - 6 + z = 0
-2x + 2y + z - 2 = 0
Нормальный вектор к (KMN): n (-2; 2; 1).
Координаты проекции точки C₁ (0; 6; 4): C₂ (x₁; y₁; z₁).
Вектор C₂C₁ (0 - x₁; 6 - y₁; 4 - z₁) ║вектору n (-2; 2; 1).
- x₁ = -2k
6 - y₁ = 2k
4 - z₁ = k
x₁ = 2k
y₁ = 6 - 2k
z₁ = 4 - k
C₂ ∈ (KMN)
-2·2k + 2(6 - 2k) + 4 - k - 2 = 0
-4k + 12 - 4k + 2 - k = 0
14 - 9k = 0
k = 14/9
x₁ = 2·14/9 = 28/9
y₁ = 6 - 2·14/9 = 26/9
z₁ = 4 - 14/9 = 22/9
C₂ (28/9; 26/9; 22/9)
Координаты проекции точки D₁ (2; 6; 4): D₂ (x₂; y₂; z₂).
Вектор D₂D₁ (2 - x₂; 6 - y₂; 4 - z₂) ║вектору n (-2; 2; 1).
2 - x₂ = -2k
6 - y₂ = 2k
4 - z₂ = k
x₂ = 2 + 2k
y₂ = 6 - 2k
z₂ = 4 - k
D₂ ∈ (KMN)
-2(2 + 2k) + 2(6 - 2k) + 4 - k - 2 = 0
-4 - 4k + 12 - 4k + 2 - k = 0
10 - 9k = 0
k = 10/9
x₂ = 2 + 2·10/9 = 38/9
y₂ = 6 - 2·10/9 = 34/9
z₂ = 4 - 10/9 = 26/9
D₂ (38/9; 34/9; 26/9)
C₂D₂ = √((38/9 - 28/9)² + (34/9 - 26/9)² + (26/9 - 22/9)²) =
= √((10/9)² + (8/9)² + (4/9)²) = √(100 + 64 + 16)/9 = √180/9 = 6√5/9 = 2√5/3.