Предмет: Математика,
автор: qwertyru2
Решите тригонометрическое уравнение и найдите все корни этого уравнения принадлежащие отрезку
а)
б)[3 ;4
;4 ]
]
Ответы
Автор ответа:
1
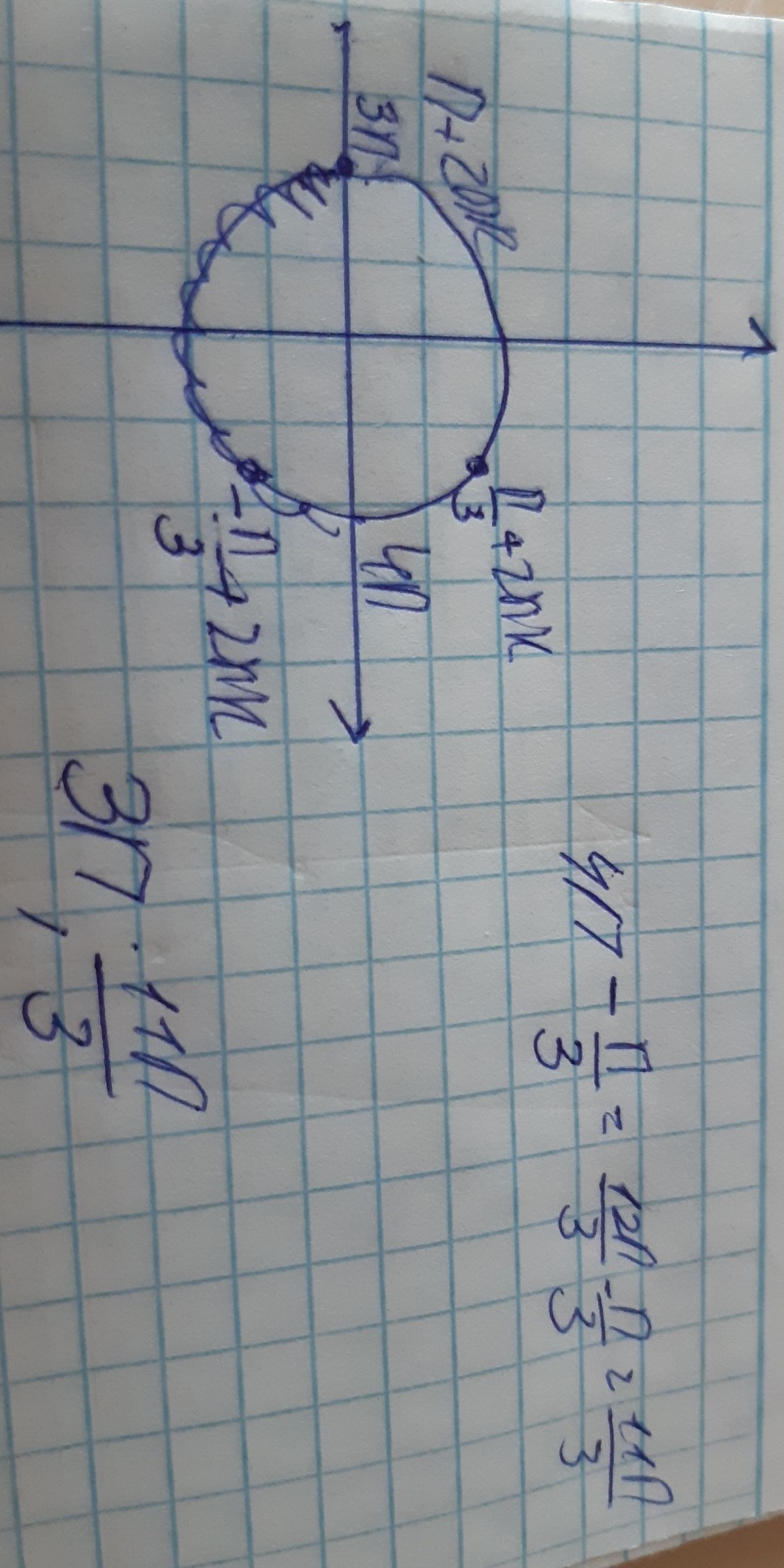
буква б во вложении
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: zshisembaevadaiana
Предмет: История,
автор: yuki83
Предмет: Русский язык,
автор: zakirovvildan
Предмет: Экономика,
автор: snezu4ka
Предмет: Геометрия,
автор: AnnaLobanova37