Question

Помогите с этой задачей!!!)) доказать я в принципе смогла, а вот как найти радиус, умоляю, помогите!!!)

Answer 1

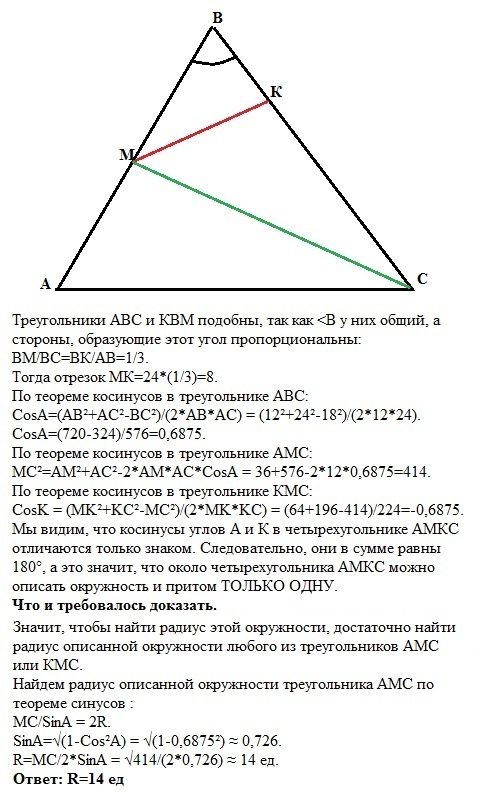
Треугольники АВС и КВМ подобны, так как <B у них общий, а стороны, образующие этот угол пропорциональны: ВМ/ВС=ВК/АВ=1/3.Тогда отрезок МК=24*(1/3)=8.
По теореме косинусов в треугольнике АВС:
CosA=(AB²+AC²-BC²)/(2*АВ*AC) = (12²+24²-18²)/(2*12*24).
CosA=(720-324)/576=0,6875.
По теореме косинусов в треугольнике АМС:
МС²=АМ²+АС²-2*АМ*АС*CosA = 36+576-2*12*0,6875=414.
По теореме косинусов в треугольнике КМС:
CosK = (MK²+KC²-MC²)/(2*MK*KC) = (64+196-414)/224=-0,6875.
Мы видим, что косинусы углов А и К в четырехугольнике АМКС отличаются только знаком. Следовательно, они в сумме равны 180°, а это значит, что около четырехугольника АМКС можно описать окружность и притом ТОЛЬКО ОДНУ.
Что и требовалось доказать.
Значит, чтобы найти радиус этой окружности, достаточно найти радиус описанной окружности любого из треугольников АМС или КМС.
Найдем радиус описанной окружности треугольника АМС по теореме
синусов :
МС/SinA = 2R.
SinA=√(1-Cos²A) = √(1-0,6875²) ≈ 0,726.
R=MC/2*SinA = √414/(2*0,726) ≈ 14 ед.
Ответ: R=14 ед.

Answer 2

Радиус находить не буду , уважаемый Andr1806 нашел его, там все просто.

А вот свое док-во представлю в файле....