Предмет: Математика,
автор: Аноним
как решать такие штуки напишите пожалуйста подробно
Приложения:
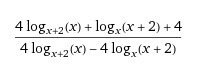
amax777:
а там в задании это не нужно чему-то приравнять?
=0
ой > или равно 0
Ответы
Автор ответа:
0
Применяем формулу перехода к другому основанию:
a>0, a ≠ 1, b>0, c>0, c≠1
Тогда
Обозначим
тогда
Применяем метод интервалов:
__-__ (-1) ___+__ (-1/2) ________-__________ (1) _+__
t < -1 или (-1/2) < t < 1
Применяем метод рационализации логарифмических неравенств:
{(x+2-1)·(x-(1/x+2)) < 0
{x>0, x≠1
{x+2>0, x+2≠1
(x+1)·(x^2+2x-1)/(x+2) < 0
D=8
x₁=-1-√2 или x₂=-1+√2
_+_ ( x₁) _-_ (-2) __+__ (-1) __-__ (x₂) _+__
С учетом второго и третьего неравенств:
(0; -1+√2)
Аналогично решаем и второе неравенство
Похожие вопросы
Предмет: Математика,
автор: dianaovcar
Предмет: Английский язык,
автор: heiskonen666
Предмет: Русский язык,
автор: yunusbadakshanov
Предмет: История,
автор: kip1501
Предмет: Геометрия,
автор: VikaFrey