Question

Решите уравнение
5cosx+4 дробь 4tgx-3=0

Answer 1

Ответ:

$x=\pi -arccos\frac{4}{5}+2\pi n$,   n∈Z

Объяснение:

$\dfrac{5cosx+4}{4tgx-3}=0$

Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю:

$\left \{ {{5cosx+4=0} \atop {4tgx-3\neq 0}} \right.$

$\left \{ {{cosx=-\frac{4}{5}} \atop {tgx\neq \frac{3}{4} }} \right.$

Решим первое уравнение:

$cosx=-\dfrac{4}{5}$

$x=\pm arccos(-\frac{4}{5})+2\pi n$

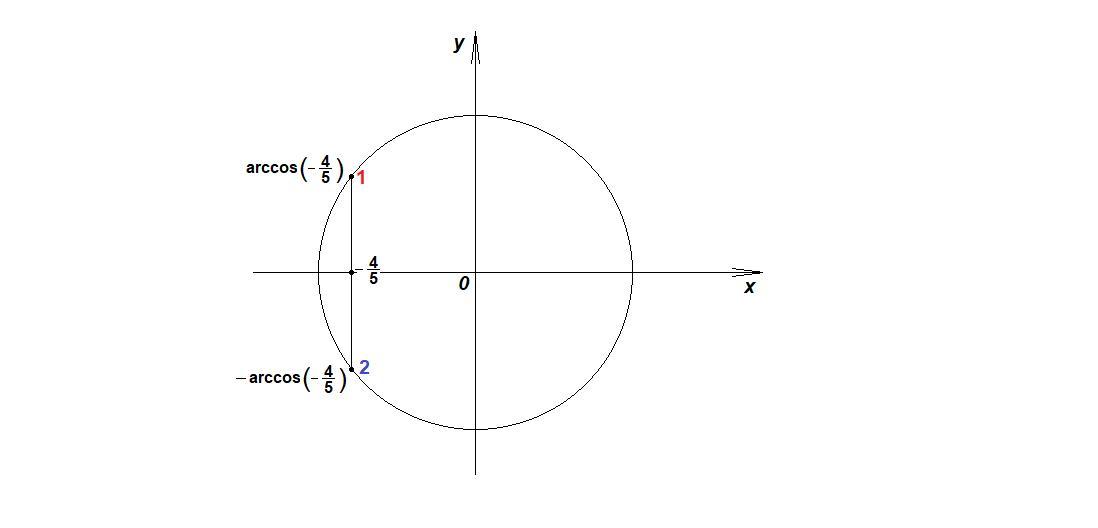
Точки, соответствующие корням уравнения, отмечены на числовой окружности.

Найдем значения tgx, если cosx = - 4/5:

$tg^{2}x+1=\frac{1}{cos^{2}x}$

$tg^{2}x=\frac{25}{16}-1$

$tg^{2}x=\frac{9}{16}$

$tgx=\frac{3}{4}$     или      $tgx=-\frac{3}{4}$

В точке (2) $tgx=\frac{3}{4}$ (так как в третьей четверти tgx > 0), а значит знаменатель превращается в нуль, значит корень

$x=-arccos(-\frac{4}{5})+2\pi n$ не подходит.

В точке (1) $tgx=-\frac{3}{4}$   (так как во второй четверти tgx < 0), значит подходит корень

$x=arccos(-\frac{4}{5})+2\pi n$

$x=(\pi -arccos\frac{4}{5})+2\pi n$,   n∈Z