Предмет: Геометрия,
автор: Знания
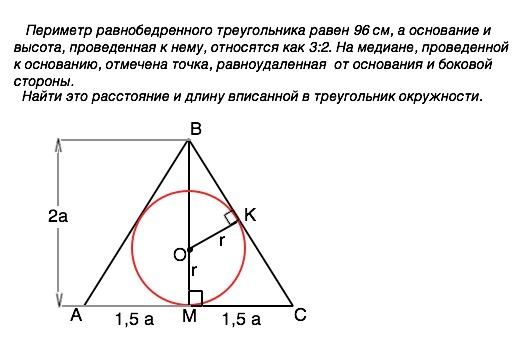
Периметр равнобедренного треугольника равен 96 см, а основание и высота, проведенная к нему, относятся как 3:2. На медиане, проведенной к основанию, отмечена точка, равноудаленная от основания и боковой стороны.
Найдите это расстояние и длину вписанной в треугольник окружности.
Ответы
Автор ответа:
3
Пусть дан треугольник АВС, ВМ - его медиана.
АС:ВМ=3:2
Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
Следовательно, медиана делит основание АС на АМ=МС, а точка на ней, равноудаленная от сторон треугольника, - центр вписанной в него окружности. ОМ=ОК=r.
Примем коэффициент отношения основания и высоты равным а.
Тогда ВМ=2а. и МС=АС:2=3а:2=1,5а,
По т. Пифагора найдем боковую сторону.
ВС=√(BM²+MC²)=√(4a²+2,25a²)=2,5a
АВ=ВС.
Р=2•2,5а+3а=8а
8а=96,⇒ а=12 см
ВМ=2•12=24 см
МС=1,5•12=18 см, АС=36 см
Формула радиуса вписанной в треугольник окружности
r=S:p, где р- полупериметр. р=96:2=48 см
r=ВМ•СМ:48=24•18:48=9 см
Длина окружности L=2πr=18π см
Приложения:
Похожие вопросы
Предмет: Математика,
автор: gogasebrakov
Предмет: Математика,
автор: danialsarbasov353
Предмет: Математика,
автор: ufe794106
Предмет: Информатика,
автор: damask89055
Предмет: Химия,
автор: BERGER11