Предмет: Алгебра,
автор: SadEast
Найти tga+cosa, если sina=3/5, a Є [90,180]
Ответы
Автор ответа:
2
Решение во вложении
Приложения:
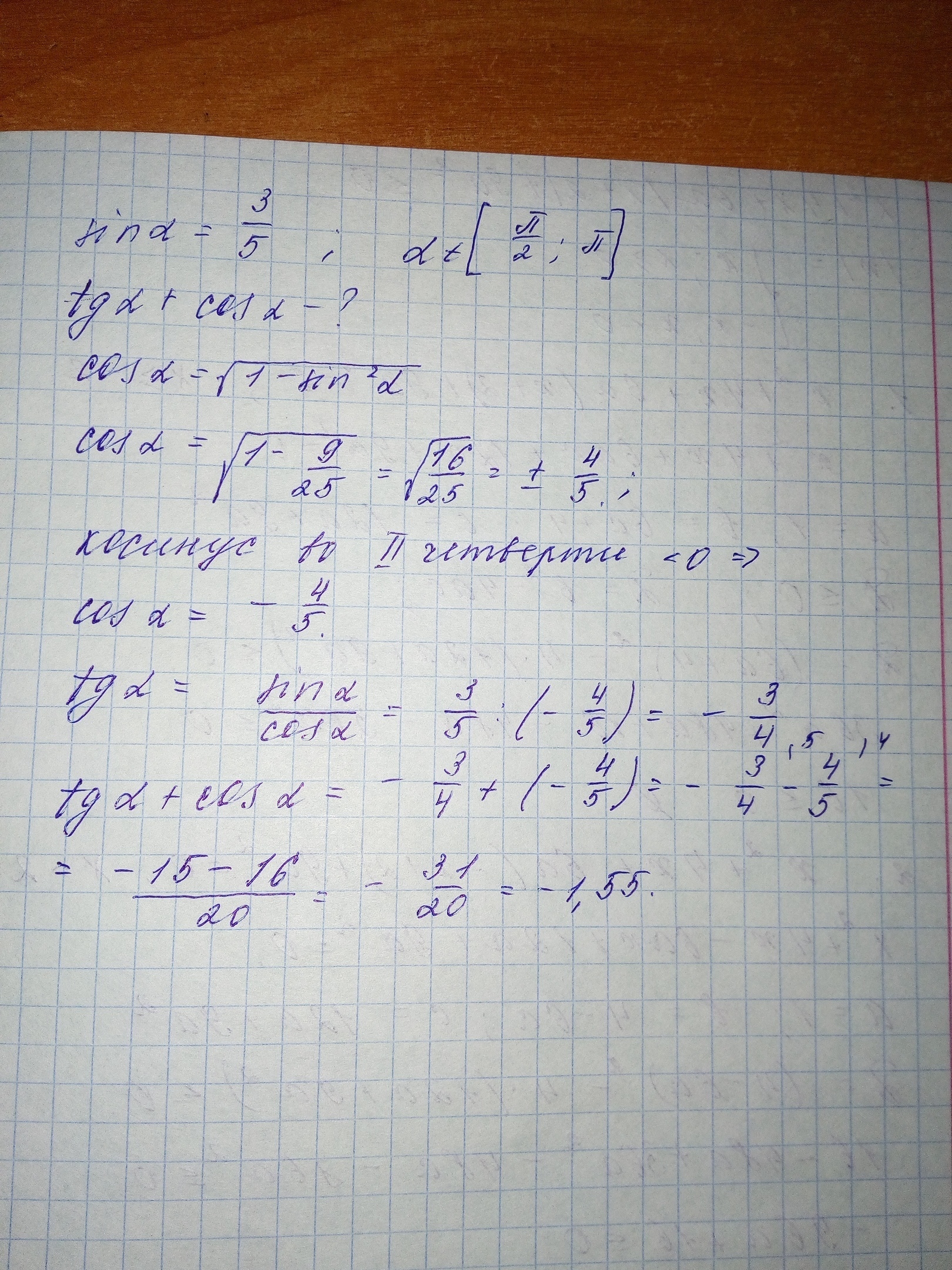
Автор ответа:
2
из основного тригонометрического тождества найдем косинус:



т. к. a Є [90,180], то косинус отрицательный

тангенс - синус делить на косинус

tga+cosa=

т. к. a Є [90,180], то косинус отрицательный
тангенс - синус делить на косинус
tga+cosa=
Похожие вопросы
Предмет: Другие предметы,
автор: Nurmeke
Предмет: География,
автор: s56712689
Предмет: Қазақ тiлi,
автор: baturinaulana6
Предмет: Химия,
автор: Аксолотльььь