Question

К графику функции y=1+3sin(2/3x)-2sinx проведены касательные, параллельные прямой y=4x+3. Найдите абсциссы точек касания

Answer 1

Угловые коэффициенты у прямых равны (у данной в задаче и у параллельных ей).

Если касательные параллельны прямой y=4x+3, то угловой коэффициент k=4.

А производная уже самой функции равна угл. коэф-ту k к графику функции y=4x+3.

Находим производную функции y=1+3sin((2/3)x)-2sin(x):

y'=2cos((2/3)x)-2cos(x)

y'=k, тогда

2cos((2/3)x)-2cos(x)=4

cos((2/3)x)-cos(x)=2

Разделим уравнение на две функции

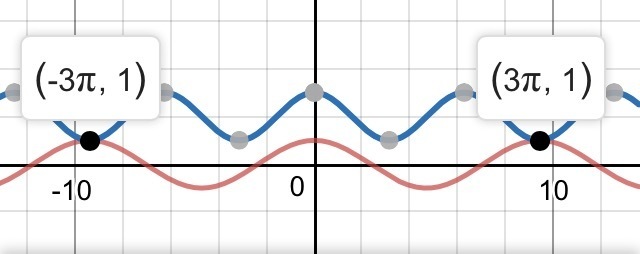
y=cos(2x/3), y=cos(x)+2 и решим его графически.

Получаем конечный ответ: x=3π+6πk (k∈Z).