Предмет: Математика,
автор: 0vvl
Решите систему неравенств

Ответы
Автор ответа:
1
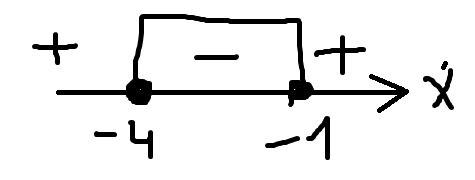
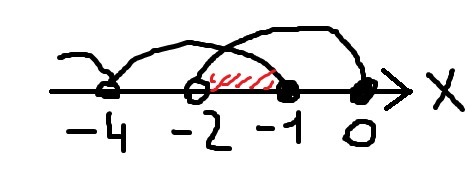
Пересечем множество решений и учтём ОДЗ (3):
Ответ: x ∈ (-2;-1]
Приложения:
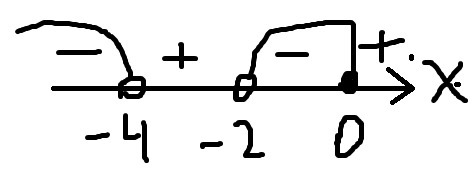
Похожие вопросы
Предмет: Биология,
автор: taisian118
Предмет: Математика,
автор: fozilbek1208
Предмет: Геометрия,
автор: Danilyandaniil
Предмет: Обществознание,
автор: 678775684
Предмет: Математика,
автор: Ferario