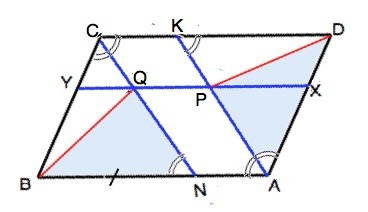
На сторонах AD и BC параллелограмма ABCD выбраны точки X и Y так что XY || AB. Биссектрисы углов A и C пересекают отрезок XY в точках P и Q соответственно. Докажите что угол ADP = углу ABQ.
Ответы
Биссектриса параллелограмма отсекает от него равнобедренный треугольник: АК делит ∠А на равные углы ∠ВАК=∠КАD; а ∠АКD=∠КАВ как накрестлежащие ⇒
∠AKD=∠КАD. Аналогично доказывается, что ∆ NBC - равнобедренный.
По условию ХY║AB.
В равнобедренных треугольниках АDК и NBC стороны ВС=BN; DК=DА, а так как ВС=AD и ∠CBN=∠ADK, треугольники CBN и ADK равны по первому признаку равенства треугольников.
Боковые стороны этих треугольников лежат на параллельных прямых, КD║BN.
. ∠BNC=∠CNB=∠KAB=∠ KAD (доказано), АК и CN по равенству соответственных углов - параллельны.⇒
Четырехугольник АNQP параллелограмм по определению (противоположные стороны параллельны), ⇒
NQ=AP
∆ ВNQ = ∆ DAP по двум сторонам и заключённому между ними углу. В равных треугольниках против равных сторон лежат равные углы.
Угол ADP=углу NBQ=углу ABQ, что и требовалось доказать.