Предмет: Математика,
автор: LinaFedorova
Помогите с решением!
log_2(x+4)>=log_(4x+16)(8)
sangers:
log₂(x+4)≥log₍₄ₓ₊₁₆₎8 - я правильно записал условие задачи?
да
Ответы
Автор ответа:
1
С учётом ОДЗ (2):
Ответ: x ∈ [-31/8; -15/4)∪ [-2; +∞)
Приложения:
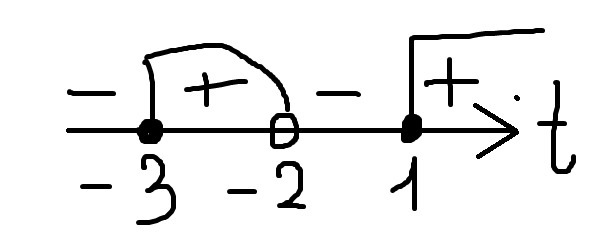

Похожие вопросы
Предмет: Математика,
автор: muftadaeleupov
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: kalabaevavenera770
Предмет: Математика,
автор: Мадина1234567890111