Предмет: Алгебра,
автор: Catdi
Помогите решить, буду благодарна, если с разъяснением
Приложения:
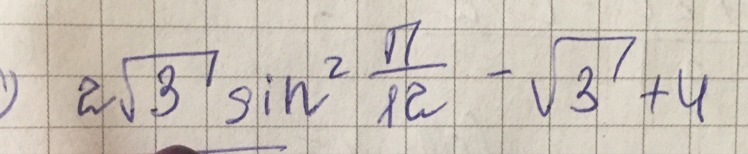
Ответы
Автор ответа:
3
1 - 2sin²x = cos2x
Ответ: 2,5
Автор ответа:
1
Используя формулу ,записать выражение в развёрнутом виде:
;
Вычислить выражение,используя таблицу значений тригонометрических функций(можно найти в Интернете) и сократить на 2:
;
Распределить √3 через скобки:
;
Сократить противоположные выражения:
;
Вычислить сумму:
Похожие вопросы
Предмет: Обществознание,
автор: restarttestartbek
Предмет: История,
автор: wertyuiopcvg15p6wjmd
Предмет: Другие предметы,
автор: sagdi8439
Предмет: Математика,
автор: умница4444
Предмет: География,
автор: любопытная11