Question

Как можно доказать, то что x=10 в уравнении 10^x=x^(10). Кроме того , что 10^10 =10^10.

Answer 1

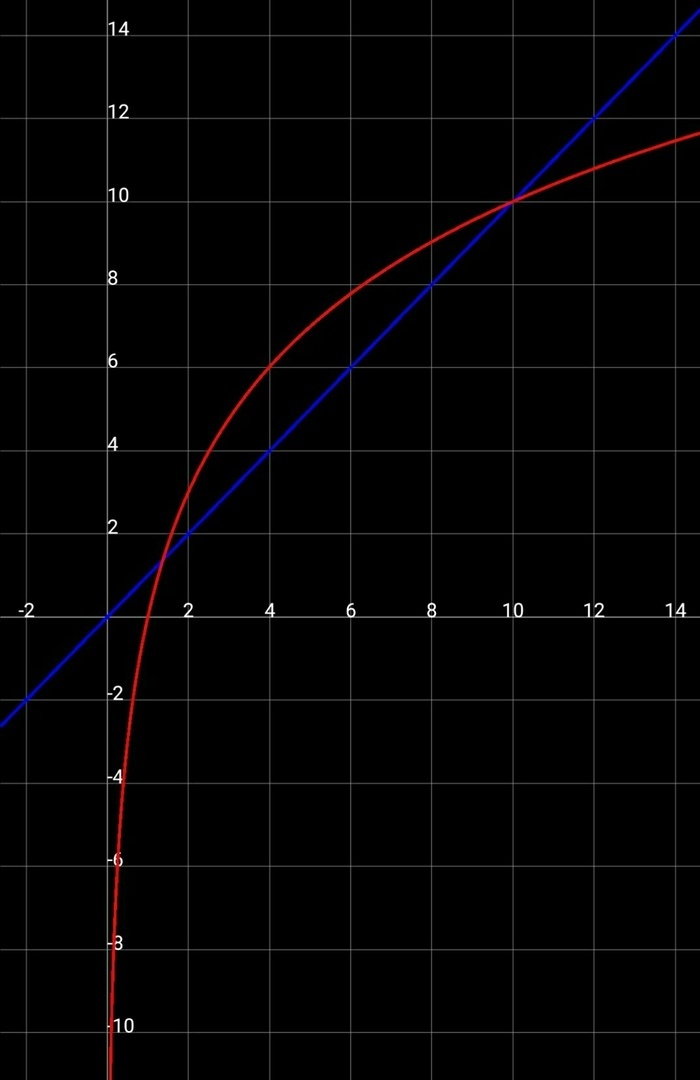
Доказать можно графически, но рассматривать графики функций y=10ˣ и у=х¹⁰ не разумно, так как обе эти функции быстро растут, поэтому перепишем данное уравнение (прологарифмируем его по основанию 10)

$10^x=x^{10} \\ \\ lg10^x=lgx^{10} \\ \\ x=10lg|x|$

а уж теперь строим графики у=х и у=10lg|x| или только для доказательство того, что есть корень 10 (х>0) модуль у логарифма можно опустить (пренебрегая отрицательным корнем). После чего получаем пересение в точке 10. Что и требовалось доказать